Forgatás testfelszín
A probléma megoldására elosztjuk az ív pont
.
Kapunk egy sokszög vonal írt egy ív. Jelöljük a hossza minden link sokszög keresztül. és ezen keresztül.
O.2.1. A hossza a görbe a korlátot, amely a beírt sokszög hajlamos hossza, amikor a hossza a legnagyobb sokszög linket nullához.
Tegyük fel, hogy a függvény folytonos, együtt az első deriváltját. És jelentésük. Ezután szerint a Pitagorasz-tétel a derékszögű háromszög lábakkal és megtalálni
.
Segítségével Lagrange-tétel, megkapjuk
.
A hossza az egész vonallánc. Mivel a függvény folytonos, a kapott szerves összeget határérték létezik, és egyenlő a hossza a görbe.
.
Így az ív hossza a görbe egy koordináta rendszer által adott
2.2. Hagyja, hogy a függvény parametrikusan tovább. azaz
. ahol; és. és a funkciók folyamatos és folytonos első deriváltja.
. .
2.3. Hagyja, hogy a görbe meghatározása a polár koordinátarendszerben
. . Képletek segítségével átmenet polárisról derékszögű koordináta-rendszer, megkapjuk:
- paraméteres görbét. Egyenletet használva (2) találunk
;
.
Ezután az ív hossza a görbe polár koordinátákkal adják
Most már mehetünk, hogy megtalálják a terület forgási felület.
Forgatás testfelszín
Ez kell számítani testfelület által alkotott forgás tengelye körül az ívelt.
Lesz osztva részek a pontokat. Csatlakozz a pontokat elosztják az akkordokat. Jelöljük a hossza az egyes akkord keresztül
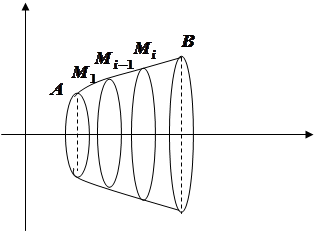
Ennek eredményeként, forgási tengelye körül minden akkord kapjunk egy csonka kúp, amelynek felülete megegyezik a termék a hossza a középső rész a kerület mentén generatix, azaz
Köztudott, hogy a. hol. ezért
A felülete a teljes ábra lesz egyenlő
A határérték ez az összeg (ha van ilyen) és az úgynevezett rotációs testfelület.
Azonban a kapott összeg nem integrált funkciót. de meg tudjuk mutatni, hogy a határ az integrál összeg erre a funkcióra egyenlő lesz a limit összege.
Átalakítás egy ponton
A paraméteres forma
A polár koordinátarendszerben