differenciálódás mátrix
Böngészi a fórumot, rábukkantam az üzenetet több mint 8 évvel ezelőtt. A jelentés azt is fel kérdéseket a nyilvánosság számára, ami általában ez csapódik le a problémát a differenciálás mentén vektor mátrix. Abban az időben az írás, a válasz, amit soha nem kapott. Ugyanakkor, most nem lát alapvető nehézség ebben a feladatban.
A probléma közös műszaki felsőoktatási intézmények a helyzet: az első évben Mesélnél a fizikai jelenségek, melyek leírása szükséges, hogy értik a rotor. gradiens. eltérés. és milyen szereplők, és hogyan kell használni őket - megmondja, másodéves.
Első pillantásra nem világos valami: az üzemeltető a differenciálódás vonatkozik a mátrixok, amelyek közül néhány több és átültetni, van differenciálódás mentén vektor, stb De ne ess kétségbe: vannak kiszámítására vonatkozó szabályok a származtatott és a mátrix nyoma és a meghatározója a mátrix termék, vagy a logaritmusa meghatározója - a mi (forumnye) esetében, ez elég egyszerű.
Először leírjuk az általános szabályok a differenciálás, ha foglalkoznak hasonló tárgyakat.
A származék vektorok skaláris - vektor az azonos méretű, amely a származékok a megfelelő elemek
A származék egy skalár f függvény a vektor x argumentumot - vektor az azonos méretű, mint x. egyenlő
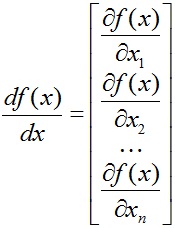
(Azaz, egy vektor, amelynek tagjai a parciális deriváltja tekintetében az elemek a x vektor.)
A származék a vektor funkció g m dimenzió a vektor érv x n dimenziós - mátrix dimenzió m × n. ahol az első sor egy részelem g1 elemeinek a vektor x, stb.:
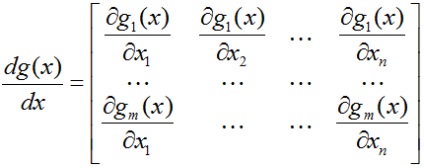
A következő két eredmény a lineáris algebra nyerhető pontosan csinál differenciálódás a szabályok szerint korábban tárgyalt. Ezek a képletek gyakran használják, így írunk, és:
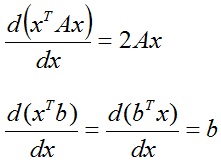
Tény, hogy megy vissza az eredeti probléma (kérdés a fórumon)
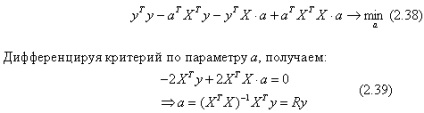
Hogyan lehet megkülönböztetni (2,38), és megszerezni (2,39)?
Tekintsük származék kifejezések (2,38).
Az első - minden nyilvánvaló a nagyon értelmében a származék:
A második kifejezés (itt használjuk a kész formulák leírt módon):
A harmadik ciklus (használjuk ugyanazt a képlet kész, de először egy kis „módosítás” kifejezés):
Ha nem érti a „átalakítás” fölött - ismét részletesebben:
Itt már használják a tulajdonságait átültető mátrixok:
Transzponált mátrix termék megegyezik a termék a átültetett mátrixok hozott fordított sorrendben.
[. ]
Dupla ültették mátrix megegyezik az eredeti mátrix
Ezekkel a tulajdonságokkal, általunk végzett reformokat, amelyek csökkentik a kifejezést egy alkalmas formában a kérelmet a végső formula.
A negyedik (használjon másik végső képletben):
Összegyűjti az összes darab együtt, és a csoport a feltételeket:
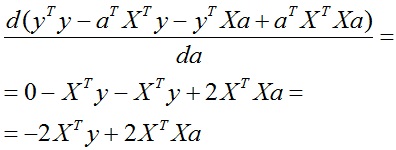
Ez az eredmény bejutottunk (2,39).