rendezési algoritmusok
Rendezési algoritmusok. 1. rész
Az összes jelenleg létező válogatás különböznek egymástól végrehajtási sebességet, az egyértelműség és a kód hosszát szépség megoldásokat. Gyakran a kód kifejlesztett egy algoritmust, hogy bármilyen változás, és így van egy csomó döntést, és amelyek közül néhány igyekszünk úgy most.
Azonban meg kell jegyezni, hogy a tanulmány az algoritmusok nem könnyű feladat, gondos vizsgálatát követeli meg minden sorban. Természetesen, ha használja a gombokat Ctrl + C, Ctrl + V, a program nem fog működni rosszabb, de véleményem szerint semmi sem rosszabb, mint amikor a programozó nem érti végéig programja működik.
kiválasztás Sort
És kezdjük a rendezési opciót. Bár ez az algoritmus nem a leggyorsabb, de úgy döntöttem, hogy kezdeni vele, mert véleményem szerint ez a legegyszerűbb megérteni. A lényege az algoritmus, hogy nem lenne a forrás tömbben, hogy megtalálják azt a legkisebb elemet, majd cserélni az első elemet a listában a talált. Miután a legkisebb a fennmaradó, és változik a második elem. És így, amíg a teljes lista.
Így szükség N + (N-1) + (N-2) +. Egy vagy N * N halad a lista rendezéséhez.
Listing 1. Válogatás Küld
Változók min és max korlátozhatja a listáról, amelyben a rendezés volt végrehajtva. Rendezni az egész tömböt kell írni a következő
2. lista Delphi / Pascal kód
SellectionSort (a, 0, magas (a));
behelyezés sort
Az is nagyon könnyű megérteni az algoritmust. Az elképzelés az, hogy hozzon létre egy új tömböt, majd egymás után illeszteni egy új tömb elemeket a régi tömböt létrehozni egy sor minden idők már elrendelte.
3. lista Rendezés betét
Ha jobban megnézed a végrehajtásáról az algoritmus, azt azonnal észre, hogy végre kell hajtani a több. mint az N * N halad, pedig ott, ahol a kód végrehajtási sebesség kritikus, hasonló algoritmust használja lejárt.
buborék Sort
A legtöbb általánosan használt válogató részben rendezett listák, mivel ez azok végrehajtási sebességet és a maximális lehet egyenlő O (N), ahol N a tömb elemeinek számát, és az O során egy menetben a hurkon. Az algoritmus a forrás listában keres egy pár követő számjegyek nincsenek rendben, majd változtatnak mestami.Protsess ismételjük, amíg nem lesz, amíg a teljes lista. Az ábra egy példát mutat adatok rendezési módszer.
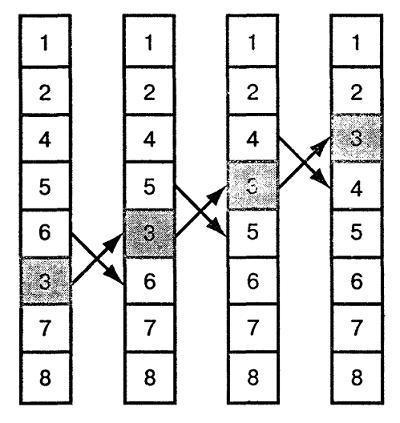
A szám lehet mozgásának követését egy elem, amely eredetileg kisebb volt, mint a válogatás után. A folyosón a ciklus az elem megváltoztatja álláspontját egy pozícióval közelebb a végleges helyére. Ábra elem tetejére mozdul, ahogy a levegő buborék a felszínre. Ez a hatás adta a nevét buborék rendezési algoritmusnak.
Listing 4 Bubble Rendezés
Quicksort.
Az ilyen típusú rendezési tömb két részre oszlik, majd felhívja magára rekurzív rendelni őket. Továbbá elemei az első részlet kisebb, mint bármely részét a második elem.
Tekintsük ezt a fajta rendezés a következő példa:
Ha az algoritmus az úgynevezett a listát, amely tartalmazza nulla vagy egy elemet, az előfizetés már rendezve, és az eljárás befejeződik, egyébként a kiválasztott egyik eleme, amelyhez képest a lista két részre oszlik, az első előfizetés kevesebb elemet tartalmaz, a második stb. És akkor, mint már említettük, hogy rekurzívan nevezi magát válogatás ailistát háttérkép.
5. lista Quicksort
Azt is meg kell jegyezni, hogy ez a fajta a legjobb használni uporyadochevaniya tömb elemeit, amelyek követik teljesen véletlenül. Mivel, ha a lista gyakorlatilag megrendelt bölcs dolog lenne, hogy egy buborék sort. Ezen felül, ha a lista elég hosszú, akkor az algoritmus okoz mély rekurzió és stoka túlfolyó, és következésképpen lógni vagy vészkijárat programot.
Rendezés Shell.
Egy másik módszer a rendezés - rendezés módja Shella.Osnovnaya ötlet ez az algoritmus, hogy az elején yctpanit tömeg zavart a tömbben, összehasonlítva sokkal egymással szemben elemekkel. Mint látható, az intervallum között összehasonlítva elemek fokozatosan csökken az egységre. Ez azt jelenti, hogy a későbbi szakaszaiban a rendezési egyszerűen a permutációk szomszédos elemek (ha, persze, ilyen permutációk szükséges).
Listing 6. Rendezze a Shell
Következtetés.
Ui Megjegyzést, javaslatot vagy kiegészítések ezt a cikket, kérjük, tegye a fórumon.