Projection egy szabályos hatszög
Nézzük meg részletesebben az építőipar egy szabályos hatszög az izometrikus nézet. Az építési kezdődik helyzetének meghatározására a szimmetriatengelye az ábra képest a tengelyek síkjának vetítés, amely egy hatszög. Tegyük fel, hogy két hatszög A és B (ábra. 86 a) az ábrán vannak merőleges sík V és szimmetriatengelye párhuzamos a tengellyel Ox és Oz.
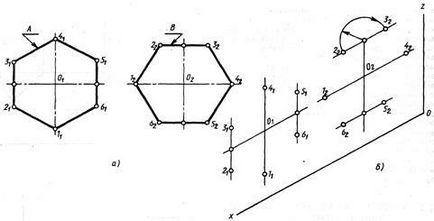
Ábra. 87 épített hatszögek N síkokban, V és W.
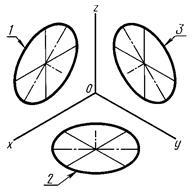
Az építési használatát igényli ellipszis mintákat. A könnyű építési ellipszis helyett egy ovális, ami épül, iránytű.
Számos módja van, hogy építsenek, úgy az egyiket. Ovális illeszkedő négy ívek: két nagy és két kicsi. A konstrukció szükséges meghatározni négy pontot, amelyen keresztül a nagy ív, és négy központi ívek.
Ábra. 89 mutatja három esetben az ovális pozícionálva axonometrikus tengelyek. Az xy síkban építési véget, a másik két sík építési megállt egy bizonyos szakaszában.
Építőipari kezdődik az ovális ovális közepén keresztül (O1 pont) vonalak a tengelyekkel párhuzamos Ox és Oz a xOz síkra; Oy és Oz a ZOY síkra; Ox és Oy XOY síkon. Ezután végezzük a kis és nagy tengelye az ovális.
A központ O1 leírják egy kör, amelynek sugara megegyezik a kör sugarát ábrázolt. Metszi a kört, és párhuzamosan futó tengely távlati egyenes kapott négy pont, amelyen keresztül halad egy nagy ív, és egy egyenes vonal, amelyen a kis tengely az ovális kapunk 1 és 2 pont, amely a központja a nagy ívek.
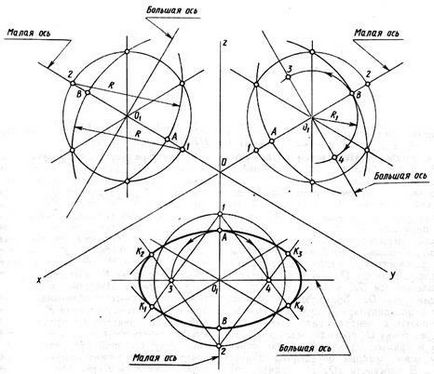
Nagy ív sugara R jelentése a távolság 1. vagy 2. pontban a pontokon, ahol a húzott kör keresztbe vonalak párhuzamos tengelyek perspektivikus (ábra. 89. xOz sík).
A további építési az ovális (gazdaság kis ívek) látható ris.89 a ZOY síkban. Fürdőzés után nagy ívben, építettek egy kis ovális tengely AB. A központ O1 sugár felével egyenlő az AB szakasz, végzett az ívet az keresztezi a fő tengelye az ovális, kap pontot a 3. és 4. Ezek a pontok központjai kis íveket az ovális. Felkutatására konjugáció kis és nagy ívű ábrán látható. 89 XOY síkon.
Geometriai test merőleges és az axonometrikus előrejelzések
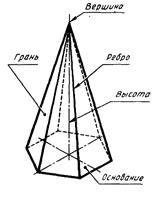
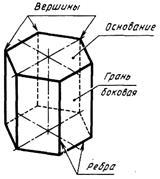
Polyhedron nevezzük prizma, amelynek bázisok poligonok, és az oldalsó felületek - négyszögek (paralelogramma vagy téglalap). prizma elemek ábrán mutatjuk be. 90, a.
Piramis nevezzük poliéder, ami fekszik az alapja a sokszög, és az oldalsó felületek háromszögek, amelyek közös csúcsa. gúlaelemek ábrán mutatjuk be. 90, b.