Lecke „mozgalom
Rövid leírása a dokumentum:
Szöveg kódolása tanulság:
Továbbra ismerős a mozgás.
Az utolsó leckében tanultunk egy újabb formája a mozgás - axiális szimmetria.
Emlékezzünk, hogy tengelyirányú szimmetria tengelyével és - leképezzük saját magára, miáltal bármely pontja K, hogy a pont szimmetrikus hozzá képest egy tengely K1.
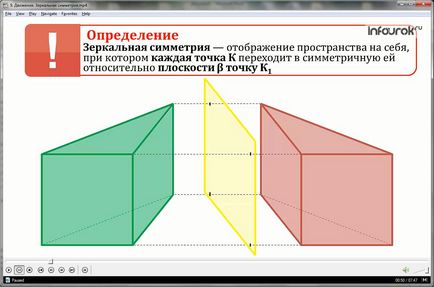
Feltérképezése saját magára, amelyben minden egyes pontban K válik szimmetrikus síkban β s pont K1 nevezett tükörszimmetrikusan (szimmetria síkkal β).
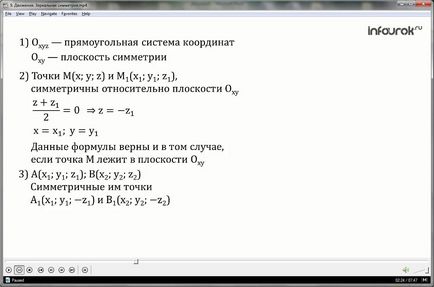
1. Be kell vezetni a Descartes-féle (derékszögű) koordináta-rendszer Oxyz úgy, hogy a Oxy síkja egybeesik a szimmetriasíkkal.
2. Keresse meg a kapcsolatot a pontok M (x; y; z) és az M1 (x1; Y1; Z1), amelyek szimmetrikusak a síkra Oxy. Ha az M pont nem tartozik egy adott síkon, a sík Oxy:
a) áthalad a középpontját a szegmens MM1;
b) merőleges a szegmens MM1.
Az első feltétel a képletek a koordinátákat a középpont, van:
z + z1 = 0, ahol z = -Z1
A második feltétel, ebből következik, hogy a szegmens párhuzamos a Z tengely-MM1 Oz. Ezért, X = x1; y = y1.
Ezek a képletek is érvényesek abban az esetben M síkjában Oxy.
3. Nézzük meg a két pont: A - koordinátái (x1; y1, z1) és B - a koordinátákat (x2; y2, z2), és bizonyítani, hogy a pontok közötti távolság az A1 és B1, hogy azok szimmetrikus, egyenlő AB.
A1 és B1 van a koordináták
A1 (x1; Y1; -Z1) és B1 (x2; Y2; -z2).
A képlet szerint a távolságok két pont között, azt találjuk:
Nyilvánvaló, hogy a hossza az AB szakasz egyenlő a hosszának a A1B1, azaz a pontok közötti távolság mentve.
Így kimutatták, hogy a tükör szimmetria egy mozgalom.
Nézzük néhány feladatot, alkalmazása a megszerzett tudást.
Bizonyítsuk be, hogy a vonalak a és a1 hazugság egy síkban, ha a tükör szimmetria vonal jelenik meg a sorban A1.
1. Mutassa be a Oxy szimmetriasíkjuk.
Úgy véljük, két esetben:
- egyenes és párhuzamos síkban Oxy.
- egyenes és nem síkjával párhuzamosan Oxy.
Abban az esetben, egyenes és párhuzamos, és Oxy sík: pontok M és L, N és K szimmetrikus (Direct tartoznak szimmetrikus), majd MA = AL, NB = BK.
Továbbá, az összes ilyen szegmensek egyenlő egymással: MA = AL = NB = BK, mert a gép Oxy - szimmetriasíkjával.
ML Közvetlen, NK - Oxy merőleges arra a síkra párhuzamos az átlagos ML NK (két egyenes vonal merőleges a síkra egymással párhuzamosan).
Így kaptunk, hogy a négyszög MLKN - egy téglalap.
Ezért, a közvetlen LK és MN párhuzamosak a szemközti oldalon a téglalap MLKN. És ez azt jelenti, hogy a vonalak a és a1, ami hazugság párhuzamos vonalak LK és a MN, párhuzamos, és ezért hazudnak ugyanabban a síkban.
QED.

2. Abban az esetben, ha a vonal nem párhuzamos sík Oxy, egyenes és metszi ezt a síkot a P pontban
Amikor szimmetria P pont leképezve önmagában, mivel ez síkjában fekszik Oxy szimmetria.
Így a P pont tartozik, és a vonal a1.
Azt találtuk, hogy a közvetlen és a1 és van egy közös pont, ezért hazudnak ugyanabban a síkban.
QED.
Tehát beláttuk, hogy a közvetlen és a1 és mindig hazudnak ugyanabban a síkban, ha a tükör szimmetria vonal, amint azt az A1 vonal.
Tekintettel a szolgáló tükör síkja szimmetriasík α p megjelenik síkban β1. Igazoljuk, hogy ha a sík párhuzamos síkban β α, β1 is a sík párhuzamos síkban α.
1. Válassza ki a három pontot az A, B, C síkban β, nem fekszenek egy sorban.
2.Dopolnitelnoe építési: tölteni szegmensek AA2, BB2, CC2 síkjára merőleges α.
Mi kiterjeszteni ezeket a szegmenseket az az A1, B1, C1, úgy, hogy A2A1 = AA2, V2V1 = BB2, CC2 = S2S1.
Van, hogy a négyszög AA1V1V - egy téglalap, mint AA1 és a BB1 = AA1║VV1 (a szimmetriasíkjai p és β1).
3. Így A1V1║AV, BB1 és CC1 = VV1║SS1 jelenti VV1S1S - egy téglalap.
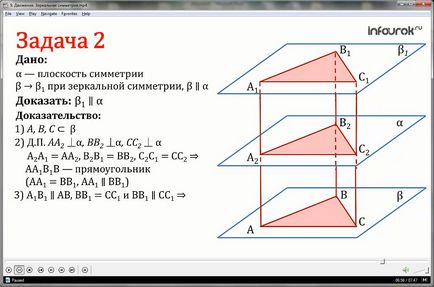
4.Ploskost β áthalad az A1, B1, C1, és ez a sík egyedülálló.
5. Ismeretes, hogy ha a metsző vonalak (BA és BC) az egy síkban (β) párhuzamos két egymást metsző vonal (V1A1 és B1C1) a másik sík (β1), akkor ezek a sík párhuzamos.
Tehát beláttuk, hogy a gépet β és β1 párhuzamosak.