A távolság a kitérő egyenes

A távolság a ferde vonalak a teljes hossza a merőleges e egyenes végzett.
Ábra. 69 látunk egy ferde vonal a és b. síkjával párhuzamosan készült az egyértelműség és. hol vannak ezek a sorok. A d távolság a sorok között a és b jelentése a hossza a közös merőleges MN.
Ábra. 69. A távolság a kitérő egyenes
Vegye figyelembe, hogy az érték a d távolság bármely pontján egy egyenes vonal a gépet (és általánosabban bármely pontjáról a gépet sík). Ezért, ha a konkrét probléma közös merőleges két kitérő egyenes nem látható, akkor kérheti távolság bármilyen kényelmes pont az első sorban áthaladó sík a második sorban, párhuzamosan az első egyenes, és ez lesz a távolság a két sor között.
12.1 Példák problémák megoldása
Tekintsük három feladatot. Az első két viszonylag egyszerű, és a harmadik megfelel a C2-es szintű a probléma a vizsga matematikából.
Probléma 1. Keresse meg a távolságot a ferde élek Egy szabályos tetraéder, amelynek a széle hossza egyenlő 1.
Határozat. ABCD egy szabályos tetraéder éllel 1. Mi található a távolság a sorok között az AD és BC. Legyen M a felezőpontja AD, N közepén BC (ábra. 70).
Ábra. 71. 2. probléma
Ezért, a távolság a két egyenes között AB és BC 1 1 a távolság bármely pontján az egyenes BC 1-D 1 1 AB síkban kényelmesen venni, például a B. pontjában
A távolság a B pont a síkra AB 1 D 1 az a távolság pont 1 legalább egy adott síkban (mivel a szegmens A B 1 ezen a síkon van osztva a felére). A távolság a 1 síkjára AB 1 D 1 A 1 jelentése a H magassága a háromszög alakú piramis AB 1 A 1 D 1.
p az alapja a piramis AB 1 D 1 egyenlő oldalú háromszög, oldalsó 2 oldalélei 3 a piramis egyenlő 3. Ezért, a piramis szabályos, és a középpontja a háromszög H 1 D 1 AB.
AH intervallum hossza megegyezik a kör sugara körülíró a háromszög AB 1 D 1:
AH = 2 p 3 = p 6: 3
Ezután szerint a Pitagorasz-tétel kapjuk:
A H = AA 1 1 2 3 AH = 2:
Ez a szükséges távolságot a sorok között az AB 1 és BC 1 p
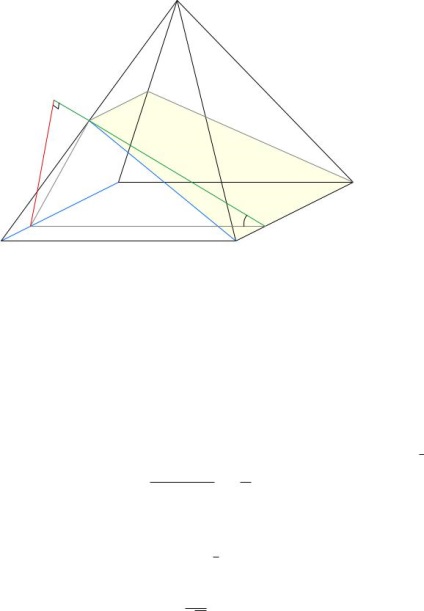
Probléma 3. A rendszeres négyszögletes piramis SABCD (a csúcs S) egyenlő a hossza az egyes borda 4. A K pont SA közepén borda. Keresse meg a távolságot a sorok között az AD és BK.
Határozat. Ábra. 72 metszeti nézete a piramis sík KBC; Ez a rész egy egyenlő szárú trapéz BKLC.