A távolság a pont a vonal a háromdimenziós térben
[Math] \ bar r_1 = (x_1, y_1, z_1) [/ matematikai] - sugara vektor egy pont a vonalon;
[Math] \ bar s_1 = (l_1, m_1, n_1) [/ matematikai] - egyenes irányvektor;
[Math] d _ [/ Math] - távolság a pont egy olyan vonalat.
[Rule] Formula
Egy pont és egy egyenes vonal távolságot képlete formájában:
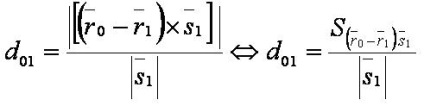
A távolság pont vonal egyenlő az arány a modul a vektor termék vektorok (r0 -R1) az S1 és a hossza a vektor s1. A geometriai jelentése általános képletű: hossza - a hossza a paralelogramma magasság (által alkotott vektorok (r0 -R1) és s1), csökkentette a bázis a paralelogramma vektorként (S1), amely egyenlő a terület aránya a paralelogramma a hossza a bázis.
Formula távolság a pont a vonal koordináta formában van:
[Rule] Példa
Adott pont és a vonal: [matematikai] (- 4; 3; 5) [/ matematikai] és [matematikai] \ frac = \ frac = \ frac [/ Math].
Keresse meg a távolságot.
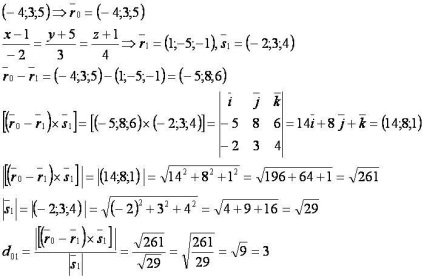
[Edit] Egyéb képletek:
[Edit] linkek
- Korn H. Korn T. Matematikai Handbook tudósok és mérnökök. M. Science 1970.
- Tag: Logic-Samara