Wolframalpha orosz bomlással a trigonometrikus Fourier sorozatba volfrám-alfa felhasználásával
A trigonometriai Fourier sorozat bővítése a Wolfram Alpha segítségével
A gyakorlatban - különösen az egyetemi hallgatók számára vagy a technikai alkalmazások esetében - gyakran szükség van a függvény trigonometrikus Fourier sorozat formájában való gyors kiterjesztésére. Ezért néhány olvasó felteszi a kérdést: hogyan kényszerítheti a Wolfram Alpha-t arra, hogy egy adott függvényt kiterjesszen egy Fourier sorozatra az oldal tetején, közvetlenül a lekérdezési mező alatt.
A válasz erre logikusan találtam.
Mivel a trigonometrikus formájában Fourier-sor Alpha Wolfram rendszere az alternatív, ez azt jelenti, hogy először kiszámítja az együtthatók exponenciális sorozat, és csak ezután átalakítja őket (leegyszerűsíti vezet trigonometrikus forma) segítségével Euler-képlet (Euler formula).
Természetesen, hogy az első expanzió a függvény trigonometrikus Fourier, meg kell, hogy azonnal tegye a rendszer pontosan ezt a feladatot, nevezetesen, hogy egyszerűsítse a bővítés a funkció Fourier-sor, ami könnyen elvégezhető a kulcsszó egyszerűsítése.
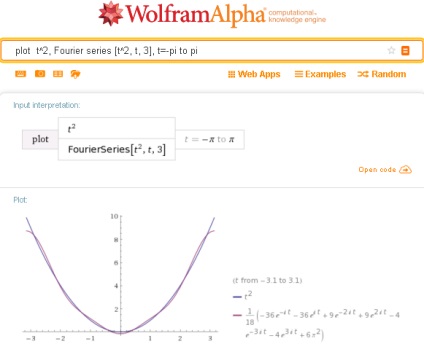
Így a függvény trigonometrikus Fourier-sorozathoz a Wolfram Alpha segítségével meg kell keresned az űrlap lekérdezését:
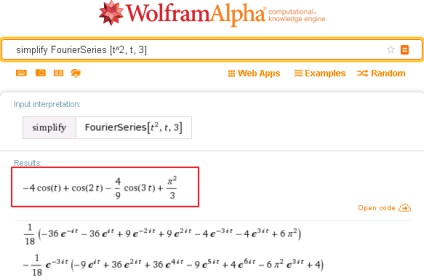
Amint az ábrán látható, itt, a rendszer első kimenetén az első 3 szempontjából az expanziós funkció t ^ 2 a trigonometrikus Fourier-sor, és másodsorban mutatja a megfelelő Fourier sor exponenciális formában.
By the way, ha hirtelen érdekel, hogy pontosan hogyan Fourier sorozat közelíti ezt a funkciót, akkor látható és egyszerűen. Elég, ha két gráfot egy koordinátarendszerben összehasonlítunk - az adott függvény grafikonját trigonometrikus közelítésével, vesszővel jelezve: