A térfeltöltő régiók fajtái
A mennyiség qV (Z) felel meg, a változás a potenciális energia a pozitív töltés az SCR értékét a relatív energia az ömlesztett félvezető (a Z, tart végtelenbe).
Az indukált töltet eloszlása egy bizonyos vastagságú rétegben azt jelenti, hogy a félvezetőben lévő potenciál egyenletesen csillapodik a felületen lévő bizonyos értéktől az SCR-n kívüli nulláig. Az elosztott térköltség nagysága (Z) és az abban levő elektrosztatikus mező potenciálja V (z) egymáshoz illeszkednek egymáshoz a Poisson-egyenlet
ahol # 949; 0 - a vákuum dielektromos állandója;
# 949; s a félvezető dielektromos állandója.
Minden olyan energiaszint, amely a félvezetőben egy adott ponton z indukált töltés hiányában létezett, az SCR értékének qV (z) értéke eltolódik.
Ha kifejezzük a potenciális energia változását a k0 T egységekben, és beviszi az Y (z) = qV (z) / (k0 T) jelölést, akkor a Poisson-egyenlet a
Mint ismeretes, bizonyos határfeltételek esetén ezen egyenlet megoldása egy bizonyos Y (z) függvény, amely mélyen beleolvad a félvezetőbe. Ennek a funkciónak a mérete a dimenzió nélküli értékeket (k0 T) az összes dimmer nélküli értékhez viszonyítja a HMO megjelenése előtt. Ugyanaz a mennyiség határozza meg az energiasávok dimenzió nélküli hajlítását minden z ponton.
Az Y (z) mennyiséget dimenzió nélküli felületi elektrosztatikus potenciálnak nevezzük.
A tiltott zenekar közepétől a Fermi szintig terjedő távolságot a betű jelöli # 981; és a felszínen lévő értéke # 981; s. Ellentétben a dimenzió nélküli elektrosztatikus potenciállal # 981; s a felületi potenciálnak nevezik. A félvezetőkre vonatkozó tudományos szakirodalomban az alsó indexet a felülethez kapcsolódó mennyiség jelenti, mivel s az angol "felületi" szó első betűje.
A találmány egy sima csillapító kapacitás változik simán minden szinten pozícióját a Fermi szintet, amely ismert, olyan intézkedés az átlagos energia a töltéshordozók egész kristályt, és ezért változatlan marad, amíg a kristály határoló (felszíni) z = 0.
A 4.3. Ábra bemutatja az IPF energia diagramját. A felületi dimenzió nélküli elektrosztatikus potenciál értékét Ys jelöli. Ennek az értéknek a jele az energiaolvasás elfogadott irányával összhangban pozitív lesz a zónák lehajlása és a kanyarok számára negatív.
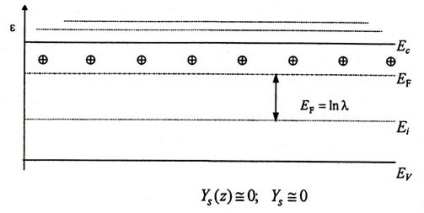
Ábra .4.3. Az elektronikus típusú vezetőképesség félvezetőjének térfelvevő régiójának energiadiagramja a felület elektrosztatikus potenciáljának tetszőleges értékére
Az ábrán jól látható, hogy a zóna hajlításának jelenlétében a Fermi energia értéke a z koordináta függvényévé válik. Ezért nyilvánvaló, hogy az SCR minden pontjára (vagy párhuzamos felületének keresztmetszetére) a statisztikai törvényeknek megfelelően az egyensúlyi koncentrációk kifejezését a
Általános megfontolásokból és a 4. ábrán látható energiadiagram figyelembevételével látható, hogy a Fermi energiát minden egyes pontnál az Ys és a Fermi energiatartomány hajlításának különbsége határozza meg a térfogatban
Ez lehetővé teszi számunkra, hogy leírjunk
A képletek (4.1.7) segítségével megkapjuk
Röviden vizsgáljuk meg a bevezetett EF és Ys jeleket. A dimenzió nélküli elektrosztatikus potenciál jelzése negatív lesz, ha a zónák felfelé hajlanak és pozitívak lesznek lefelé hajlítva. EF. és az Ys-nek is negatív jele lesz, ha a Fermi szint a tiltott sáv alsó felében lévő energia diagramon van, és fordítva.
A kapcsolatok (4.2.7.) Valójában tükrözik a Maxwell-Boltzmann statisztikák használatát az ns és ps felületi koncentrációk meghatározásához. Korábban már említettük, hogy nagyon közel van az engedélyezett zónához. A közelségi tényezőt a (4.1.1.) Képlet nevezőjének egységkijelzője közötti arány határozza meg. Ha az exponens nagyobb, mint 3, akkor az exponens nagyságrendje nagyobb, mint az egység - a Boltzmann statisztikához való átmenet. Ellenkező esetben degenerációra kerül sor, és szükség van a Fermi statisztikára.
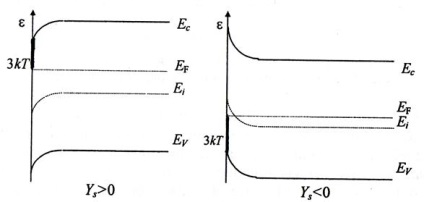
Ábra. 4.4 Energiagramok, amelyek korlátozzák a zóna íveket
A felületet, ez azt jelenti, hogy a figyelembe kell venni a sávban hajlító, amelyben a felszínen a Fermi szint közelebb van a széleit a megengedett sávok közelebb, mint 2-3 k0 T.
A határolókések a 4. ábrán látható grafikonokban láthatók
Vizsgáljuk meg a felületeken keletkező különböző típusú HMO-kat, először kvalitatív módon, még a Poisson-egyenlet megoldása előtt is. Példaként válasszunk egy felületi SCR képződését egy félvezetővel, amely elegendően hangsúlyos n-típusú vezetőképességgel rendelkezik. Ez azt jelenti, hogy az egyenlőtlenség EF = ln # 955;> 3 tartja érte.
1. Lapos területek. Ezt a helyzetet az energia diagramon ábrázoltuk közvetlen zónákkal a felszínig (4.5 ábra). A felszíni Fermi-szint helyzete megegyezik a térfogat térfogatával. A térköltség területe nem alakul ki: # 961; (z) = 0
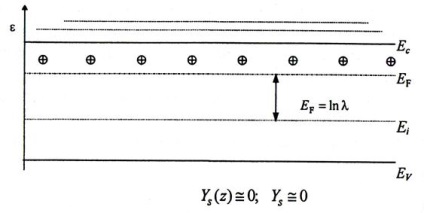
Ábra 4.5. Energiadiagram a sík zónák esetében (a térfeltöltő terület hiányzik)
2. Dúsítás. Meg kell jegyeznünk, hogy ez és minden további kifejezés a fő töltéshordozók koncentrációjának változására utal. Például a vizsgált esetben nyilvánvaló, hogy a dúsítás a fő hordozók koncentrációjának növekedését jelenti az OPZ felületén. Ezt a régiót a fő töltéshordozó-n (z)> n0 "dúsította". Példaként kiválasztott elektron-félvezető esetében ez azt jelenti, hogy a Fermi-szint a felületen és a teljes térfeltöltési tartományban közelebb van a vezetési sávhoz, mint a tömegben. Mindez megfelel a zónák hajlításának. A választott referenciarendszerben ez megfelel az Ys> 0 felszíni elektrosztatikus potenciál pozitív értékének (4.6. Ábra).
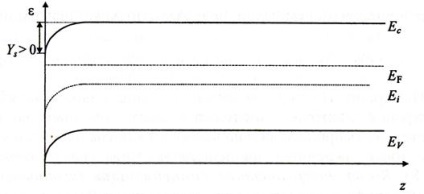
Ábra 4.6. Az n-típusú félvezető felszínének energiadiagramja, amely megfelel a ns> n0 dúsítás eseteinek
Ha az ns felületi koncentráció nem túl nagy, mint n0. akkor ez egy rossz gazdagodás. Ez megfelel az Ys kanyarulatainak
Ha Ys> 3, erős dúsítás fordul elő ns >> n0 esetén. Nyilvánvaló, hogy amikor a lyukak koncentrációjának gazdagítása a térfeltöltési tartományban kisebb, mint a térfogatban, mivel egyensúlyban mindig np = ni 2.
3. A kimerülés. A fenti meghatározásnak megfelelően ez az állapot azt jelenti, hogy az SCR-ben az elektron koncentráció kisebb, mint az n (z)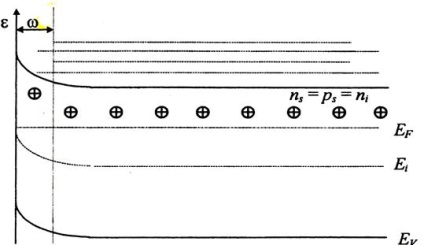
4.7 ábra. Az elhasználódásnak megfelelő n-típusú félvezető felület energiadiagramja
A zónák hajlításának további növekedésével jön egy idő, amikor mind az elektronok, mind a lyukak koncentrációja elhanyagolható az ionizált donorok koncentrációjához képest. Következésképpen ezek a mozgatható donorok alkotják a felszíni töltés nagy részét. A felszíni Fermi szint egybeesik a tiltott sáv közepén Ys = ln # 955; Az elektronokat ugyanolyan mélységgel visszük vissza a térfogatba, ami korlátozza a kimerültség egyértelműen kimondott réteget (4.7 ábra).
A térfogat és a felületi koncentráció aránya ebben az esetben
4. Inverzió. Mivel a zónák negatív hajlítása növekszik, az elektron koncentrációja tovább csökken, és a lyuk koncentráció nő. Ez a folyamat nagymértékben felgyorsul, miután a Fermi szintje a tiltott sáv közepén a felszínen átesett (4.8 ábra)