A tomográfia és az ultrahangos hangzás matematikai vonatkozásai

Tekintsük a CT probléma főbb jellemzőit a transzmissziós tomográfia példáján keresztül.

A síkon lévő problémára korlátozódunk - amikor egy objektum térbeli szerkezetét két koordinátának függvényében írjuk le, és rekonstrukcióját egy függvény (előrejelzés) egy csoportjával végezzük.

Hagyja, hogy az I0 intenzitású röntgensugarak síkja áthaladjon az objektumon (lásd az 1. ábrát) az (X, Y) síkban. Tegyük fel, hogy S

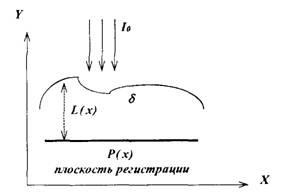
Ábra. 1. Az átviteli tomográfia rendszere

egy abszorbeáló közegen keresztül. Tegyük fel, hogy az objektum csillapítási tényezője állandó: 8 (y) = c> "= const.

Ezután a tomográfia legegyszerűbb feladata (az inverz probléma) az objektum alakjának és Sg értékének az I (x) függvény elérése.

Ha az abszorbens közeg egy kis rétege áthalad A-on, akkor a sugárzási intenzitás változása arányos a réteg vastagságával és a csillapítási együtthatóval:

Ha a függőleges koordináta mentén integráljuk (1) a sugár keresztmetszetét képező sugarak mentén, megkapjuk az objektum képét a regisztrációs síkban:

A transzmissziós tomográfia alapja az (2) kifejezés: az ismert F (x) függvényből meg kell szerezni a g (y) # 9632; S (y) = S0 = const esetén az integráció (2) hozama.

Még ebben legegyszerűbb esetben a megoldás a probléma csak akkor lehetséges, bizonyos feltételek mellett: így a tárgy alakját (az L (x)) kell tudni az értékét csillapítási tényező, vagy éppen ellenkezőleg, hogy megtalálják a csillapítási tényezőjének kell tudni, hogy az a tárgy alakja. Ezenkívül a probléma ezen megfogalmazásában végtelen számú olyan objektum van, amely a regisztrációs síkban ugyanazt a P (x) vetületet adja. Valóban, ha az alsó határa az objektum nem lapos, a vastagsága az egyes funkciók b (x) felel meg, végtelen számú tárgyak különböző alakú. Ha besugározza az objektumot egy másik irányból, a vetítés a felvételi síkban más lesz, de a probléma a bizonytalanság a helyreállítás a tárgy marad. Így egy tárgy helyreállítása megkívánja, hogy információt szerezzünk a különböző szögekből nyert vetületekről. Előzetesen azt kell feltételeznünk, hogy a tárgy egy olyan test, amelynek állandó csillapítási együtthatója van benne. Vagy szükségünk van egy sokkal nagyobb számú képre az objektumról. Következésképpen, az inverz probléma megoldásához előzetes információra van szükség (a priori - latinul - "az előzőtől"). Ez a tulajdonság a tomográfia problémáinak abszolút többsége. A matematikában ezeket a problémákat rosszul mondják [17]. Ezek alapvető tulajdonságait - a bizonytalanság a határozatot, valamint az a tény, hogy a végtelenül kicsi hibák a kezdeti adatok hibákhoz vezethet a végső számítások eredménye [7, 11]. Egy egyszerű példa: kis változások a csillapítási tényezője S (v) az expressziós (2) miatt az integráció a gerenda L (\) vezethet jelentős változásokat a képrögzítő sík P (x).

Az inverz problémák megoldásának módszereinek fejlesztése a modern matematikai fizika és diszkrét matematika nagy része. A gyakorlati alkalmazásokban az ilyen elméleti vizsgálatok lehetővé teszik a különböző tomográfiai típusok optimális beolvasási rendszereinek létrehozását [6, 14]

A vizsgált transzmissziós tomográfia mellett emissziós tomográfiát alkalmaztunk. A nukleáris medicina, optikai és radioteplotáció (radiometria) [5, 14]. Ellentétben emissziós tomográfia van az, hogy ez egy tipikus példája a passzív mérési -, hogy információkat kapjon az objektum által használt saját sugárzás (X-ray, optikai, mikrohullámú sütő), [5, 14]. Például a nukleáris medicinában a feladat a radioaktív készítmény térbeli eloszlása ​​a szervezeten belül a szervezeten kívüli sugárzási intenzitásnak megfelelően. Mint minden problémát passzív hullám érzékelés, ez a feladat bonyolultabb a fent tárgyalt, a sík esetben kifejezés helyett (2) a képfelvételt síkban fog kinézni:

ahol a a sugárforrás aktuális koordinátája, F

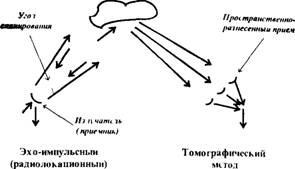
2. ábra A visszhang-impulzus eltérése a tomográfiás vizsgálati módszertől

Az akusztikus tomográfia (AT) a szétszóródás és a refrakció inverz problémáinak megoldására alapul.

Az akusztikus tomográfia és a hagyományos echo-impulzus (radar) ultrahangos hangzás közötti különbség vázlatosan látható a 2. ábrán. 2.

Mindkét esetben az objektum szögletes beolvasását feltételezzük, azonban szerkezetének rekonstrukcióját tomográfiai módszerrel feltételezzük, szükség van egy térbeli távolságú hangjelzésre. Leggyakrabban AT-ben a geometriai optika közelítését alkalmazzák (sugárközelítés), ebben az esetben a közeg információforrása nem a csillapítási tényező, hanem a hang terjedési sebessége. A fizikai szempontból a szóródás és a refrakció inverz problémái csak az inhomogenitás természetében és az alkalmazott közelítésekben különböznek (3.

A közeg homogenitása a természetben lévő hullámok terjedésében az irányt tekintve # 1141; a térbeli változás határozza meg

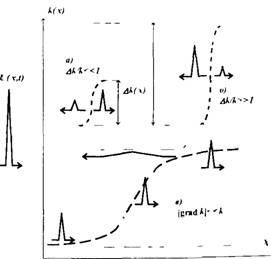
I. ábra A hullámszórás alapváltozata egy inhomogén közegben

ahol ω a ciklikus frekvencia, és c (n) a hullámterjedési sebesség. Ha a méret a inhomogenitás összehasonlíthatók a hullámhossz, akkor a visszavert hullám amplitúdója által meghatározott sebesség és szakaszosan, illetve a hullám száma IGEN (g) (felső része ábra. 3.). Az A k / k «1 állapotban a tranziens energiája

a későbbi inhomogenitás térbeli pozícióját gyenge visszavert jelben rögzítjük, attól függően, hogy a vevőben milyen visszaverődő hullám érkezik. Az ilyen közelítést a Born-approximáció, vagy az egyszórás [2, 4, 8] által a hullámok elméletében nevezzük. A visszhangos impulzusos hangosítási módszerrel a legtöbb esetben ezt a közelítést használják. Ellenkező esetben (IGEN „/ K” 1) hullám nem szaporodik belsejébe a vizsgálati tárgy és a tárgy hullám érzékelhető, hogy információt kapjunk a alakja annak határát, nem a belső szerkezetét. A tapintás, különösen az ultrahangos készülékek felbontása nő az ω frekvenciával. Itt, az ultrahang-hullámok frekvenciával nő, és a csillapítási együttható 8 W „[13], amely elvileg korlátozza a térbeli sávja ultrahangos készülékek.

Sima, inhomogén közeg esetén, amikor az inhomogenitás méretei sokkal nagyobbak, mint a hullámhossz ((gradk («κ.

Ábra. Ábra), a visszavert jel gyakorlatilag hiányozhat, és az inverz problémák megoldásához a törésmutató elveit alkalmazzák. Ilyen problémák esetén a hullám-jelek fázisa a sugárzás (pályák) mentén integrálódik. Ebben az esetben a sugarak olyan görbék, amelyek alakja a közeg sebességétől (törésmutatójától) függ. Ez a törésmutató a kívánt mennyiség, amelynek térbeli eloszlását vissza kell állítani. Kezdeti adatok ilyen feladatok időbeli késedelmek (fázis) wave jelek mentén terjedő különböző sugarakkal vagy ray beesési szögnél a különböző pontjai a térben. Módszerek fénytörési Tomográfia elterjedt szeizmológiai (vizsgálatára a földkéreg), légköri fizika (visszaállítani a nagy magasságban a légköri paraméterek annak lámpázást egy optikai vagy rádiófrekvencia), óceántan (helyreállítása sűrűség profil, sótartalom, hőmérséklet az óceánok mélységét feltételei alapján hang hullámok) [3, 15, 19, 21, 22].

Tekintsünk két alapvető elméleti megközelítést az inverz hullámproblémák megoldására.