A motor létrehozása a 3d rendereléshez a Java-on

A 3D-s renderelés, a játékokban és a multimédiában használt modern motorok a matematika és a programozás szempontjából meglepőek. Ennek megfelelően kiváló munkájuk eredménye.
Sok fejlesztő tévesen úgy gondolja, hogy a legegyszerűbb 3D-s alkalmazás létrehozása a semmiből szükségessé teszi a több embert ismereteket és erőfeszítéseket. Szerencsére ez nem teljesen igaz. Továbbá, ha van számítógéped és szabadidőd, magad is létrehozhatsz hasonló dolgokat. Vessünk egy pillantást a saját 3D-s renderelés motorjának fejlesztésére.
Természetesen, ha nagyszerű 3D-s alkalmazást szeretne létrehozni sima animációval, akkor jobban használja az OpenGL / WebGL alkalmazást. Az alapvető ötlet azonban az, hogy az ilyen motorok hogyan működnek, és sokkal összetettebb motorokkal dolgozik.
Ebben a cikkben megpróbálom elmagyarázni az alapvető 3D-rendering a helyesírási vetítés, egy egyszerű háromszög raszterizációs (a fordított folyamat vektorizálási), Z-Buffer és lapos árnyékolás. Nem fogok összpontosítani a figyelmet olyan dolgok, mint optimalizálási, textúrák és a különböző fényviszonyok között - ha szükség van rá, próbálja ki alkalmasabb erre a célra olyan eszközök, mint az OpenGL (van egy csomó könyvtárak, amelyek lehetővé teszik, hogy a munka az OpenGL, akkor a Java).
A kód példái Java-ban lesznek, de maguk az ötletek természetesen alkalmazhatók bármely más nyelven, amelyet választott.
Elég beszélgetés - menjünk üzletbe!
Először tegyünk valamit a képernyőn. Ehhez egy olyan egyszerű alkalmazást fogok használni, amely a rendezett képünket és a két forgatógombot forgatja.
Az eredménynek így kell lennie:

Most adjunk hozzá néhány modellt - csúcsokat és háromszögeket. A csúcs csak egy struktúra a három koordináta (X, Y és Z) tárolására, és a háromszög összekapcsolja a három csúcsot és színüket tartalmazza.
Itt feltételezem, hogy X jelentése jobbra-balra, Y-felfelé, és Z lesz a mélység (úgy, hogy a Z tengely merőleges a képernyőre). A pozitív Z jelentése "közelebb áll a felhasználóhoz".
Példaként a tetraédert választottam a legegyszerűbb alaknak, amire emlékszem - csak 4 háromszögre van szükség ahhoz, hogy leírhassa.
A kód is elég egyszerű - csak 4 háromszöget hozzunk létre és adjuk hozzá az ArrayListhez:
Ennek eredményeképpen egy olyan alakot kapunk, amelynek a középpontja a (0, 0, 0) eredetű, ami meglehetősen kényelmes, hiszen a számot ezzel a ponttal forgatjuk.
Most adjuk hozzá a képernyőhöz. Először is, nem adjuk hozzá a forgatási képességet, és csak húzzuk meg az ábrán a drótkeret ábrázolását. Mivel ortográfiai kivetítést használunk, elég egyszerű - csak távolítsuk el a Z koordinátát, és húzzuk meg a háromszögünket.
Ne feledje, hogy most már elvégeztem az átalakításokat a háromszögek rajzolása előtt. Ez úgy történik, hogy központunk (0, 0, 0) a képernyő közepén helyezkedjen el - alapértelmezés szerint az eredet a képernyő bal felső sarkában található. A fordítás után meg kell kapnia:

Lehet, hogy nem hiszed, de ez a tetraéder a merőleges vetítésben, őszintén!
Most forgatni kell. Ehhez egy kicsit távolabb kell elmennem a témáról, és beszélni kell a mátrixok használatáról és arról, hogyan érhetem el őket 3D-s pontok 3D átalakításával.
A 3D-s pontok manipulálására sokféle mód van, de a legrugalmasabb a mátrixszaporítás. Az ötlet az, hogy a pontokat 3 × 1 méretű vektor formájában mutassuk be, és az átmenet valójában 3 × 3 mátrixszal szorzódik.
Vegyük az A bemeneti vektorunkat:
És szaporítsuk azt az úgynevezett T transzformációs mátrix segítségével, hogy megkapjuk a B kimeneti vektort:
Így például az, hogy mi lesz az átalakulás, ha 2-tel szorozzuk:
Nem lehet leírni semmilyen lehetséges átalakítást 3 × 3 mátrix segítségével - például ha az átmenet a téren kívül történik. 4 × 4 mátrixot használhatsz, 4D-térbe hajlítva, de ez nem szerepel ebben a cikkben.
Az itt használt átalakítások skálázása és forgatása.
Bármely forgatás 3D térben 3 primitív rotációban fejezhető ki: az XY síkban való elforgatás, az YZ síkban való elforgatás és az XZ síkban való elforgatás. Mindegyik rotációra transzformációs mátrixokat írhatunk a következőképpen:
És itt van, ahol a varázslat kezdődik: ha szüksége van, hogy először egy forgáspont az XY síkban a transzformációs mátrix T1, majd végezze el a forgatás ezen a ponton az YZ síkban a transzformációs mátrix T2, akkor egyszerűen szorozza meg a T1-T2 és megszerezni egy mátrix, amely leírja a teljes forgatást:
Ez egy nagyon hasznos optimalizálás - ahelyett, hogy folyamatosan számolnánk a forgatásokat minden ponton, előzetesen egy mátrixot feltételezünk, majd használjuk.
Nos, elég ijesztő matematika, menjünk vissza a kóddal. Hozzunk létre egy Matrix3 szolgáltatási osztályt, amely kezelni fogja a mátrix-mátrixot és a vektor-mátrix-szorzatokat:
Most meg tudod és ébresztheted a forgatásunkat. A vízszintes görgő szabályozza a forgatást balra és jobbra (XZ), és a függőleges görgő vezérli a forgatást felfelé és lefelé (YZ).
Hozd létre a rotációs mátrixunkat:
Szintén hozzá kell adnia a hallgatókat a görgetőkhöz annak biztosítása érdekében, hogy a kép frissüljön felfelé vagy lefelé vagy jobbra-balra húzva.
Amint azt már észrevette, a felfelé és lefelé való bejutás nem működik. Adja hozzá ezeket a sorokat a kódhoz:
Eddig csak a figuránk csontvázát ábrázoltuk. Most töltsük be valamit. Ehhez először meg kell raszterizálnunk a háromszöget - hogy megjelenítsük képpont formájában a képernyőn.
Az a gondolat, hogy kiszámoljuk a háromszög belsejében található minden pixelre vonatkozó baricentrikus koordinátát, és kizárjuk azokat a kívülről. A következő töredék egy algoritmust tartalmaz. Figyeld meg, hogyan jutunk közvetlenül a képponthoz.
Rengeteg kód, de most van színes tetraéder a képernyőn.

Ha játszol a demóval, észre fogod venni, hogy nem minden tökéletes - például a kék háromszög mindig magasabb, mint mások. Ez azért van, mert háromszögünket egyenként vonjuk be. A kék az utolsó, ezért a tetejére húzódik.
Javítsd meg ezt, fontold meg a Z-pufferelést. Az ötlet egy raszterizálási folyamat közbenső tömb létrehozása, amely megtartja a távolságot az egyes képpontok utolsó látható elemére. Doing háromszög raszterizációs fogjuk ellenőrizni, hogy a távolság kevesebb pixel a távolság, mint az előző, és a festék is csak akkor, ha ez található a másik tetejére.
Most nyilvánvaló, hogy a tetraédernek van egy fehér oldala:

Így van egy működő motor a 3D-s rendereléshez!
De ez nem a vég. A valós világban a szín érzékelése a fényforrások helyzetétől függően változik - ha csak kis mennyiségű fény esik fel a felületen, akkor sötétebbnek tűnik.
A számítógépes grafikában ezt a hatást az úgynevezett "árnyékolással" érhetjük el - a felület színváltozását a fényerő forrásához viszonyított dőlésszög és távolság függvényében.
Az árnyékolás legegyszerűbb formája lapos árnyékolás. Ez a módszer csak a felület, a normál és a fényforrás irányát veszi figyelembe. Csak meg kell találni a szög koszinusát a két vektor között, és szorozza meg a színt a kapott értékkel. Ez a megközelítés nagyon egyszerű és hatékony, ezért gyakran használják nagy sebességű megjelenítésre, amikor a legfejlettebb árnyékolási technológiák túlságosan hatékonyak.
Először is meg kell számolnunk a háromszög normál vektort. Ha ABC-háromszögünk van, normál vektort kiszámíthatunk az AB és AC vektorok vektortermékének kiszámításával, és az eredményül kapott vektort hossza szerint.
A vektortermék bináris művelet két vektoron, amelyek így definiáltak a 3D térben:
Itt van egy vizuális ábrázolás, amit a vektortermünk tesz:
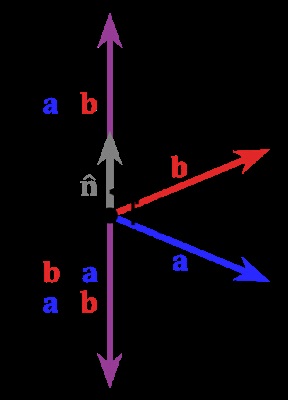
Most számolni kell a koszinuszt a háromszög normál és a fény iránya között. Az egyszerűség kedvéért feltételezzük, hogy a fényforrás található, közvetlenül a kamera mögött bármilyen távolságban (egy ilyen konfiguráció az úgynevezett „irányított fény”) - így, a mi fényforrás azon a ponton (0, 0, 1).
A vektorok közötti szög koszinusa a következő képlet segítségével számítható ki:
Ahol || A || A vektor hossza és a számláló az A és B vektorok skaláris terméke:
Megjegyezzük, hogy a fény irányának vektorának hossza egyenlő 1-gyel, valamint a háromszög normál hossza (már ezt normalizáltuk). Így a képlet egyszerűen átalakul erre:
Figyeljük meg, hogy csak a fény irányának Z-összetevője nem nulla, így egyszerűen mindent egyszerűsíthetünk:
A kódban mindez triviálisnak tűnik:
Elhagyjuk az eredményjelzőt, mert célunkra nem számít, hogy a háromszög melyik oldala néz a kamerára. Valódi alkalmazásban nyomon kell követnie ezt, és ennek megfelelően alkalmazni kell az árnyékolást.
Most, miután megszereztük az árnyékoló tényezőt, alkalmazhatjuk háromszögünk színére. Egy egyszerű verzió így fog kinézni:
A kód ad nekünk árnyékoló hatásokat, de sokkal gyorsabban csökken, mint amire szükségünk van. Ez azért van így, mert a Java az sRGB színspektrumot használja.
Ezért minden színt lineáris formátumra kell konvertálni, árnyékot kell alkalmazni, majd vissza kell konvertálni. Az igazi átmenet az sRGB-ről az lineáris RGB-re meglehetősen időigényes folyamat, ezért nem fogok teljes feladatlistát végrehajtani. Ehelyett valamit meg fogok tenni ehhez.
És most látjuk, hogyan animálja a tetraéderünk. Van egy működő motor a 3D-s rendereléshez színek, világítás, árnyékolás, és körülbelül 200 sornyi kódot vett igénybe - nem rossz!
Itt van egy kis bónusz az Ön számára - gyorsan létrehozhat egy alakot, amely közel van a gömbhöz a tetraéderből. Ezt úgy érhetjük el, hogy mindegyik háromszöget 4 kisebb méretűre törjük és "felfújjuk".
Íme, mit kell kapnia:

Ezt a cikket befejezem azzal, hogy szórakoztató könyvet ajánlok: "A 3D-s matematika alapjai a grafika és játékfejlesztés számára". Ebben a folyamatban a renderelési folyamat és a matematika részletes magyarázata található. Érdemes elolvasni, ha érdekel a rendereléshez használt motorok.