Több áramkörű visszacsatolási rendszer
Multi-loop visszacsatolási rendszer.
Egy többszörös hurok visszacsatolási rendszer megnyitása egy átviteli függvény megszerzésére tetszőleges helyen végezhető el.
A b / a megnyitása az első link bemeneténél (a fő átviteli függvény megszerzéséhez):
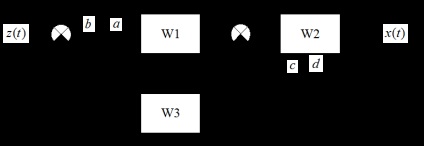
Átviteli funkció (fő):
.
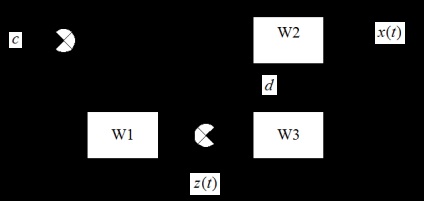
.
Az átviteli funkciók különbözőek. Mindazonáltal a zárt rendszer jellemző egyenletei megegyeznek:
,
.
Így a stabilitás meghatározásához a rendszer átviteli függvényét használhatjuk úgy, hogy a kezdeti rendszert tetszőleges pontban megnyitjuk. Azonban csak a fő átviteli függvény kapcsolódik a zárt rendszer átviteli funkciójához a jól ismert relációval:
.
Attól a ténytől, hogy a zárt rendszer stabilitásának vizsgálatakor csak a jellemző egyenlet érdekel
,
ebből következik, hogy a stabilitás kiszámításához transzformált átviteli függvény használható
,
ahol az önkényes polinom több, mint a polinom mértéke.
.
Többdimenziós vezérlőrendszerek [1].
A többdimenziós rendszerek azok, amelyeknek több beállítható értéke van:
, ().
A többdimenziós vezérlő objektumot egy egyenletrendszer írja le, amely általában egy mátrix formában jelenik meg:
, , .
Itt u. f - kontroll és zavaró hatások (vektorok).
Mozgás egyenletei mátrix formában:
.
, ,
- a kezelői együtthatók négyzetes és négyszögletes mátrixa.
Laplace képek esetén (zéró kezdeti feltételek mellett):
.
Itt vannak ellenőrzött mennyiségek, kontroll mennyiségek és perturbációk képeinek mátrixoszlopai.
Ha a meghatározó, akkor van egy inverz mátrix. Az eredeti egyenletet a bal oldalon szorozzuk meg:
- az objektumátviteli függvények mátrixa a szabályozási változók és zavarok számára.
Az inverz Laplace transzformáció megtalálásával az objektum átviteli függvényeinek mátrixainak minden egyes elemére az úgynevezett Cauchy mátrixot (tömegfüggvények mátrixát) kapjuk. Például az ellenőrzési műveletekhez
.
Ha az adott pillanatban minden bemenet ellenõrzõ tevékenységet kap, akkor a j-os vezérelt változó változását a Duhamel-Carston integrál segítségével rögzítjük:
.
Az alábbi ábra egy zárt, többdimenziós automata vezérlőrendszer blokkdiagramját mutatja. Pontosan ugyanaz, mint egy egydimenziós rendszer, csak g, x, u, y, f vektorok, "mátrixok".
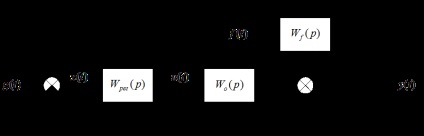
Az átviteli funkciók mátrixa nyitva van a rendszer összes csatornáján:
.
A rendszer jellemző mátrixa egy négyzetes méretű mátrix, E az identitás mátrix:
.
A jellemző mátrix meghatározója a jellemző egyenlet:
.
Zárt rendszer átviteli funkcióinak mátrixai, véletlenül zárt rendszer és perturbációval zárt rendszer:
, , .
A kétdimenziós rendszer stabilitása antiszimmetrikus korlátokkal.
A kétcsatornás nyomkövető rendszer blokkdiagramja:
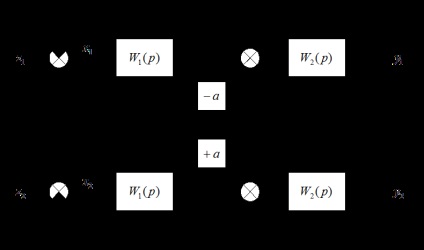
A kimeneti (állítható) értékek kapcsolata hibásan:
.
.
.
.
A stabilitás vizsgálata két egyenlet figyelembe vételével csökkenti:
Itt a Nyquist kritérium használható, de a komplex sík () pontjának helyett, amely megfelel a jellemző egyenlet szokásos rögzítésének, két komplex számot és pontot kell figyelembe venni.
Egy zárt rendszer stabil lesz, ha az elszigetelt csatorna nyílt állapotban lévő AFC nem fedezi a pontokat és.
Egy oszcillációs stabilitási határ megtartja, ha az egyenlők egyike vagy teljesül.
Vegyük észre, hogy mindkét pontban u egy pontra mutat, ami megfelel a Nyquist-kritérium szokásos megfogalmazásának.
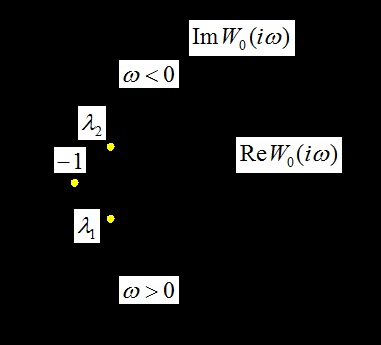
Egy másik módszer a kétdimenziós rendszer stabilitásának kiszámítására.
Bevezetünk. Voltak arányok:
.
A második egyenlőséget megszorozzuk i-vel, és hozzáadjuk:
.
Itt van egy nyitott kétdimenziós rendszer ekvivalens átviteli függvénye, az átviteli függvény forgási szöge az óramutató járásával megegyező irányba és a modul modulusa.
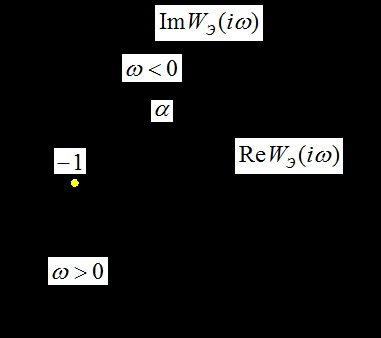
Az oszcillációs stabilitási határ: amely csökkenti a
.
Ez összhangban van a stabilitás kiszámításának első módszerével.