Az infinitezimális, infinitezimális táblázat összehasonlítása
A függvények infinitezimálisak, ha, mivel x az a pontig terjed, a határuk 0.
Az infinitezimális funkció azonban csak egy bizonyos ponton lehet. Amint az 1. ábrán látható, a funkció csak a 0. pontban van infinitezimális.
1. ábra: Végtelenül kicsi funkció
Ha a két függvény hányadosának határértéke 1-et eredményez, akkor a függvények egyenértékűek az infinitesimális értékkel, míg az x a.
Ha az f (x), g (x) függvény infinitesimal értéke $ x> a $, akkor:
- Az f (x) függvényt a g (x) -hoz viszonyítva végtelenül kicsinek tekintjük, ha a következő feltétel teljesül: \ [\ mathop \ limits_ \ frac = 0 \]
- Az f (x) függvény az n n-edihez képest végtelenül kicsi ahhoz képest, hogy g (x), ha különbözik a 0-tól és a korlát véges: \ [\ mathop \ limits_ \ frac (x)> = A \]
A $ y = x ^ 3 $ függvény végtelenül kicsi az x> 0-nál magasabb rendű, az y = 5x függvényhez képest, mivel az arányuk 0, ez azért van, mert a $ y = x ^ 3 $ függvény nulla gyorsabb érték:
Az y = x2-4 és y = x2-5x + 6 függvények infinitízimálisan kicsiek x> 2-vel azonos sorrendben, mivel az arányuk nem 0:
Az egyenértékű infinitezimális tulajdonságai
- A két egyenértékű infinitezimális különbség mindegyikhez képest magasabb rendű infinitezimális.
- Ha a különböző megbízások több infinitesimáljának összegéből a magasabb rendű végtelen számokat vesszük el, akkor a fennmaradó rész, amelyet a fő résznek nevezünk, egyenértékű a teljes összeggel.
Az első tulajdonságból következik, hogy az egyenértékű infinitezimális értékek megközelítőleg egyenlőek lehetnek az önkényesen kis relatív hibával. Ezért a ≈ jelet egyaránt használják az infinitezimális egyenértékek egyenértékének megadására és a kellően kicsi értékek közelítő egyenlőségének leírására.
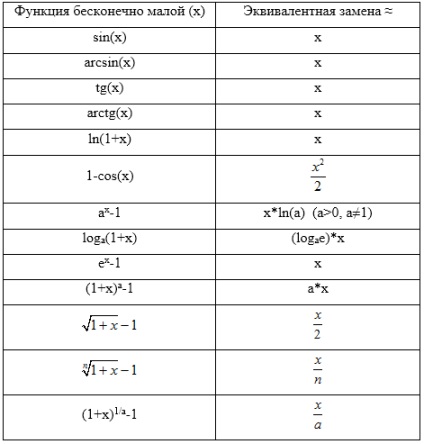
A határértékek megállapítása során gyakran szükséges az egyenértékű funkciók helyettesítésére a számítások gyorsasága és kényelme miatt. Az ekvivalens infinitesimals táblázatot az alábbiakban mutatjuk be (1. táblázat).
A táblázatban megadott infinitesimális egyenértékűség igazolható az egyenlőségre támaszkodva:
Az egyenértékű értékek helyettesítése