A fogalmak közötti kapcsolat
A koncepció tartalma mellett a kötet is.
Példák. A "szék" fogalma magában foglalja az összes széket, az "asztal" fogalmát - minden táblázatot.
Kötetei még az olyan egyszerű fogalmakat, mint „szék” és „asztal” homályosak, homályos, és ezért ezek a fogalmak pontatlanok. Sőt, ott jön egy szék vagy egy asztal, amely csak a tervek szerint nem az ács, a hatálya alá a „szék” fogalmát, vagy „asztal”? A „felügyelő” Nyikolaj Gogol említ egy tanár, aki beszélt a Nagy Sándor, olyan forró, hogy tört székek. Ezek a törött székek a "szék" fogalmának hatálya alá tartoznak? Ezeket és hasonló kérdéseket nehéz egyértelműen megválaszolni.
Két önkényes fogalom köre között, amelyek valamilyen értelemben összehasonlíthatók egymással, a következő kapcsolatok közül csak egy van:
benyújtás (két lehetőség)
Az egyenértékűek két koncepciót jelentenek, amelyek teljes köre teljes.
Más szavakkal, az egyenértékű fogalmak ugyanazt az objektumosztályt jelentik, de sok szempontból ezt teszik.
Egy példa. Az egyenértékűek a "négyzet" és az "egyenlőtlen négyszög" fogalmai: minden négyzet egyenlő oldalú négyszög, és fordítva.
Az ekvivalencia két koncepció kötetének egybeesését jelenti, de nem tartalmuk.
Egy példa. A fogalmak "fiú" és "unokája" egybeesnek, mert minden fiú valaki unokája, és minden unokája valaki fia, de tartalmuk más.
A fogalmi kötetek közötti kapcsolatok geometriai formában ábrázolhatók körrendszerek segítségével. A XVIII. Századi matematikus Leonard Euler (1707 - 1783) "Euler körök" néven hívják őket. A kör minden egyes pontja egy objektumot jelent, amely a vizsgált fogalom körébe tartozik. A körön kívüli pontok olyan objektumokat jelentenek, amelyek nem tartoznak ebbe a koncepcióba.
A két egyenértékű fogalom kapcsolata két teljesen egybeeső kör alakjában jelenik meg.
A kereszteződés tekintetében két olyan koncepció létezik, amelyeknek a kötetek átfedik egymást.
Egy példa. A "pilóta" és az "űrhajó" fogalmainak metszéspontjai metszenek: egyes pilóták űrhajósok (a körök árnyékolt részei). Vannak olyan pilóták, akik nem űrhajósok, és léteznek űrhajósok, akik nem pilóták.
Az alárendelést tekintve olyan fogalmak, amelyek egyikének mennyisége teljesen bejut a másik kötetébe.
Egy példa. Az alárendeltség tekintetében a "háromszög" és a "téglalap alakú háromszög" nevek: minden háromszög háromszög, de nem minden háromszög négyszögletes.
Egy példa. Az alárendelést tekintve a "nagyapa" és a "unokája" fogalmai: minden nagyapám valaki unokája, de nem minden unokája nagyapák. A "unokája" alárendelt fogalom, a "nagyapa" alárendelt.
Ha az alárendeltségre vonatkozó általános fogalmak vannak, akkor az alárendelt fogalmat nemzetségnek nevezik. és a látás alárendeltje.
Példák. A "háromszög" fogalma egyfajta "téglalap alakú háromszög", és a "unokája" fogalma a "nagyapa" formája.
Ami a kirekesztést illeti, léteznek olyan fogalmak, amelyek teljes mértékben kizárják egymást.
Példák. A "trapéz" és "ötszög", "ember" és "bolygó", "fehér" és "vörös" és hasonló kifejezések kizárják egymást.
Kétféle kivétel létezik.
1. A kizáró mennyiségek oly módon kiegészítik egymást, hogy azok a nemzetség teljes mennyiségét adják, amelyik a faj. A fogalmak, amelyek mennyiségei kizárják egymást, kimerítik az általános koncepció hatókörét, ellentmondásosak.
Példák. Ellentmondásosak a "ügyes" és "kemény", "tartós" és "instabil", "gyönyörű" és "csúnya" fogalmak és hasonlók. A "vörös" és a "nem piros" fogalmak, amelyek kimerítik a "színes tárgy" általános fogalmát, ellentmondanak egymásnak.
2. Az exkluzív fogalmak csak abban az összegben vannak, amilyen nagyságúak azok a fajok, amelyeknek fajai. A fogalmak, amelyeknek kötetek kizárják egymást, anélkül, hogy kimerítenék az általános koncepció körét, ellentétesnek tekintendők.
Ellentmondásos fogalmak
Példák. Az ellenkezője a "vörös" és a "fehér" fogalma, nem pedig kimerítik a "színes tárgy" általános fogalmát.
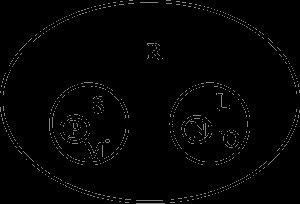
Körsémák alkalmazhatók egyidejűleg több mint két fogalom térfogati viszonyainak megjelenítésére. Az ábrán a fogalmak köre közötti összefüggést ábrázoló diagram látható:
"Planet" (S), "exoplanet" (P), "Föld" (M);
"Műhold" (L), "mesterséges műhold" (N), "hold" (O);
"A mennyei testünk galaxisunkban" (R).
E rendszer szerint léteznek olyan égitestek, amelyek nem vagy bolygók, sem műholdak. Az egyes fogalmak kötetét pontok képviselik.