Az egyenletek gyökereinek közelítő számítása, matematikai problémák megoldása
Az egyenletek gyökereinek közelítő számítása
Feladat: Válasszuk el az egyenlet egy gyökereit, és számítsuk ki a kapott intervallumon [a; b] 0,0001 értékre három módszerrel.
A) a dichotómiás módszer
B) egyszerű iterációs módszer.
D) Az akkordok módszere.
megoldás:
a) megoldja az egyenletet egyszerű iterációs módszerrel
Mi megosztjuk a gyökeret, ezért átalakítjuk az egyenletet a formára:
és hozzon létre funkciókat grafikonokat.
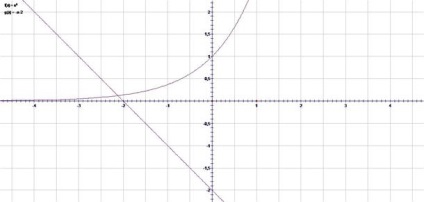
Ezen grafikonok metszéspontja a [-3; -2] intervallumon látható; Ezzel az intervallummal keressük a gyökeret.
Az egyenletet formává alakítjuk
.
Az első közelítést választjuk.
így a szükséges pontossággal
b) megoldja az egyenletet a dichotómiás módszerrel (a szegmens elválasztása, amelyen a gyökér el van választva, félig).
egyenlet:
A szegmens, amelyen a gyökeret keressük [-3; -2].
egy szegmens végein a funkció különböző jeleket mutat
Vegye figyelembe a [-2,5; -2] intervallumot a végén a funkció különböző értékeket vesz fel a jelhez.
Tekintsük a szegmenst [-2, 25; -2], mivel a végén a funkció különböző értékeket vesz fel a jelhez.
Tekintsük a [-2,125; -2] intervallumot; a végén a funkció különböző értékeket vesz fel a jelhez.
Tekintsük a [-2,125; -2,0625] intervallumot; a végén a funkció különböző értékeket vesz fel a jelhez.
Vegye figyelembe a [-2,125; -2,09375] intervallumot a végén a funkció különböző értékeket vesz fel a jelhez.
Tekintsük a [-2,125; -2,109375] intervallumot, mivel a végén a funkció különböző értékeket vesz fel a jelhez.
Tekintsük a [-2,125; -2,1171875] intervallumot; a végén a funkció különböző értékeket vesz fel a jelhez.
Tekintsük a szegmenst [-2,12109375; -2,1171875], mivel a végén a funkció különböző értékeket vesz fel a jelhez.
Tekintsük a [-2,12109375; -2,119140625] intervallumot; a végén a funkció különböző értékeket vesz fel a jelhez.
mert , akkor a gyökér megtalálható egy adott pontossággal
D) megoldja az egyenletet az akkord módszerrel.
egyenlet:
Az iterációs képlet a következőképpen alakul:
A gyökér egy adott pontossággal található meg
következtetés:
Ennek az egyenletnek a megoldásában a gyökerek háromféleképpen alakulnak ki:
A függvény egyenlete értéke: ezeken a pontokon megegyezik
0.00003163
-0.00008037
Ie nem nagyon különbözik a nullától. Az első, második és harmadik esetben a gyökerek jelentette különbségek magyarázata az iteratív folyamat leállításának különféle kritériumai