A sztereó kép mélységi térképének ábrázolása a GPU-n valós időben -
A STEREO MÉDIAKÁRTYA SZÁMÍTÁSA GRAFIKAI FOLYAMATRÓL REAL TIME-BEN
Kotyuzhansky L.A. 1
1 FGAOU HPE "Ural Szövetségi Egyetem nevezték el az első elnök az orosz BN. Jelcin, Jekatyerinburg
Javasoljuk a nagysebességű módszert egy sztereó kép mélységi térképének kiszámítására, amelynek minden egyes képpontja tartalmaz információt a sztereó kamerától való távolságról, grafikus processzoron (GPU) történő megvalósítás céljából. Ez a megoldás az adaptív struktúra több csúszó ablakának használatán alapul, a bemeneti és kimeneti képek elő- és utófeldolgozásával. Nagy teljesítmény érhető el a modern GPU-k architektúrájának köszönhetően, amelyek a legmegfelelőbbek a mélységi térkép helyi módszerekkel történő kiszámításának problémájával. Az algoritmus futási idejének összehasonlítása a központi processzoron (CPU) és a GPU-n a javasolt megoldás nagy skálázhatóságát mutatja. A nagy sebesség lehetővé teszi ezt a módszert valós idejű feladatok végrehajtásában, például a robotikában és a természetes interfészek létrehozásában. E módszer lehetséges javításának módjait tárgyaljuk.
3. Harris J. Fast Fluid Dinamika Szimuláció a GPU-n / J. Harris // http.developer.nvidia. com / GPUGems / gpugems_ch38.html.
4. Harris J. Prins J. Nyland L. Gyors N-test szimuláció CUDA / J. Harris / Prins J / Nyland L // GPU drágakövekkel 3 31. fejezet.
A sztereó látás egyik fontos feladata a két sík kép háromdimenziós jelenetbe való átalakításának folyamata, a lapos kép minden pontjának mélységére vonatkozó információk helyreállításával (a sztereó kamera és a valós kép helyzete közötti távolság).
A mélységi információk ismerete (két változó funkciója) segítségével 3D-s modelleket és egyéb természetes objektumokat hozhat létre különböző alkalmazásokhoz, például a virtuális valósághoz, a repülésszimulációhoz, a robotikához. Különösen a tudás a távolság képpontok az igazi prototípus lehetővé teszi, hogy a mozgó objektum referencia pontot szerezni háromdimenziós koordinátáit, ami fontos a speciális effektusok ipar, film és televízió. GCP koordináta rögzítési lehetővé teszi, hogy építsenek egyedülálló érintés nélküli ember-gép interfész, ellenőrzés, ahol a mozgás az ujjak, vagy akár gesztusok térben bizonyos távolságra a sztereó kamera.
Jelenleg aktív és passzív módszerek vannak arra, hogy visszanyerjék a valós jelenet mélységéről szóló információkat. Az aktív módszerek ultrahangos átalakítót vagy a munkafelület lézersugárzását használják, amely gyors és pontos információt szolgáltat a mélységről a kimeneten [2, 6]. Azonban ezek a módszerek korlátozottak a mérési tartomány és a hardverelemek költségei tekintetében.

Ábra. 1. A mélységi térkép kiszámításához használt általános eljárás
Ennek a munkának az a célja, hogy kidolgozzon egy módszert és egy szoftvermodult az elfogadható minőségi mélységi térkép kiszámításához a legrövidebb időintervallumokban, az olcsó eszközök 10-40 milliszekundumában. Ezeket a követelményeket az a tény teszi szükségessé, hogy ez a modul más szoftvermodulokkal való interakcióra szolgál, amelyek feladata nyomkövetési objektumok, arcok és gesztusok azonosítása. Valamennyi modulnak valós időben kell működnie egy PC-n, egyetlen szoftveres rendszerben, amely az emberi forgalmat és az érintés nélküli multimédiás vezérlést tartalmazza.
A számítások általános sorrendjét az 1. ábra mutatja. 1. A bemeneti adatok előfeldolgozásából, a kimeneti adatok képpontkülönbségének és végső utófeldolgozásának kiszámításával a medián szűrőből áll.
A számítások első lépése a sztereopária gradiens képeinek a konvolúciós módszerrel való előállítása (2. Ábra) [5]
Itt Ci a bal oldali kép feldolgozott képpontja; Ii (i. J) - az eredeti pixel a bal oldali képen; N (x Y) egy 3 × 3 pixeles szomszédság; M (i. J) az ismert konvolúciós mátrix eleme
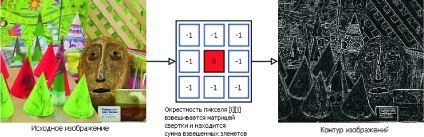
Ábra. 2. Kontúrok kiválasztása a képen
Ezt követõen kiszámítjuk a gradiens és a forrásképek lineáris kombinációját változó paraméterrel k (3.
Az ilyen előfeldolgozás jelentősen csökkenti a hiba valószínűségét a pixel mélységének kiszámításakor, különösen akkor, ha homogén, alacsony kontrasztú területek vannak a sztereó páron (4.
A képpont d definíciója közötti különbség megegyezik a bal és a jobb oldali kép képpontja közötti távolsággal (a megfeleltetés a kiválasztott y képsoron sorról-képpontra történő feldolgozással történik)
Itt xl az y fixvonal kiválasztott pixele helyzete a bal oldali képen, xr a jobb oldali képen lévő megfelelő pixel pixel helyzete.
Ahhoz, hogy megtaláljuk xr-t, a jobb oldali y vonal minden eleméhez (x. Y) a C pontok értékeinek összegét számítjuk ki a környéken, amint azt a [8] mutatja.
ahol W (x. y) egy vagy kétdimenziós szomszédság (ablak) pixelek középpontja (x y).
A költség alatt a bal (kiválasztott) és a jobb (felkapott) képpont közötti különbség modulját értjük:
Itt p a bal oldali kép pixelje; q a jobb képen lévő képpont; d - választható eltérés.
Ezután a jobb oldali képen lévő koordinátákkal (xl-d. Y) rendelkező pixel helyének megfelelő legkisebb értéket a számlálás módszerével kapott összes összegből választjuk ki. Ezt az elvet sokféle változatban alkalmazzák, különösen az adaptív ablak megvalósításában [8]. Tehát a vízszintes vonal mentén a bal és a jobb oldali képen a leginkább hasonló képpontok és azok környezetei képezik a minimális költségeket.
A helyi módszerek méretének növelésével a csúszó ablak, egyrészt, csökkenti a hibák előfordulásának valószínűsége annak meghatározásában a különbség a pixel, és másrészt, jelentősen növeli a számítás, ami miatt ez a módszer kevéssé alkalmas számításai sztereopárokból nagyfelbontású valós időben. Ezenkívül megjelenik az előtér "puffadásának" hatása (4. ábra).
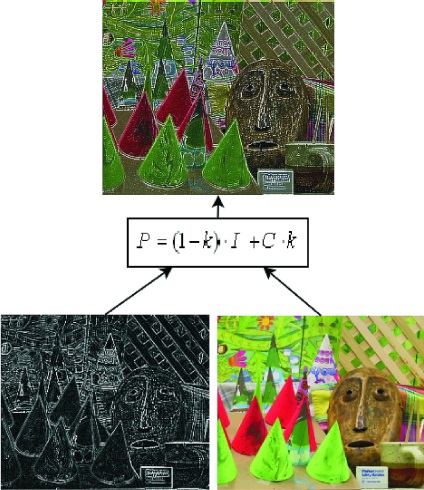
Ábra. 3. k = 0,5; P - feldolgozott pixel, az eredeti kép I - képpontja: a gradienskép C - pixelje

Ábra. 4. A bemeneti adatok előfeldolgozásának előnyei - a mélységi térkép kiszámítása előfeldolgozással (balra)
Ha olyan ablakokat használ, amelyek adaptív struktúrával rendelkeznek, akkor a mélységi térkép jó minőségű lesz, de még mindig nagyszámú számításra van szüksége.
A javasolt eljárás szerint a gyorsaság és a minőség optimális egyensúlyának elérése érdekében két egydimenziós, gyér ablakot használnak - függőlegesen és vízszintesen. Minden ablak a képpont középpontjától függ. A vákuum alatt érthető, hogy az ablak nem egymás legközelebbi pixeleiből áll, hanem olyan pixelekből, amelyek bizonyos távolságra vannak egymástól, például két, négy, hat pixel. Ez lehetővé teszi a számítási sebesség lényeges növelését a hiba jelentéktelen növekedésével (5.
Két egyszemélyes költség kiszámításához
Ábra. 5. A mélységi térkép elkészítésének különböző változataihoz tartozó számítások eredményei: a - ablak 3 × 3 - számítási idő 7,6 ms; b - ablak 10 × 10 - 125 ms; c - ablak 21 × 21 - 700 ms; d - két egydimenziós, gyér ablak 20 × 1, hígítási lépése 4 pixel - 11,7 ms
A következő képleteket használják:
Itt Wh és Wv a pixel (x. Y) középpontú pixel vízszintes és függőleges szomszédai; Ch a vízszintes ablak költsége; Cv - a függőleges ablak költsége; Cd - a teljes költség a ponton (x - d. Y).
Hangsúlyozzuk, hogy a fenti képletekben az összegző műveletet az összegző indexekhez viszonyítva végezzük el, egy olyan lépcsővel változtatva, amely nem egyenlő az egyikel (az ablak degenerációs hatása (szomszédság)).
Ennek a módszernek a kidolgozásakor felismertük azokat a módszereket, amelyek javíthatják a minőséget és optimalizálhatják a számítás sebességét. Tehát a mélység szinte teljes eltávolításához és az objektumok határainak élességének növeléséhez a mélységi térképen a bemeneti kép szegmentálása használható. Ez lehetővé teszi, hogy megtalálja a mélységi térképet nem a kép egyes pixeljein, hanem a kép szegmens síkjára. Egy másik megközelítés az, hogy a javasolt algoritmust feldolgozzuk csak a kép érdekes területein, vagy a mélységérték kiszámítását csak a mozgó objektumok számára a sztereó kamera keretén belül.
Grebennikov V.I. Doktora fizikum-matematika. Professzor, vezető kutató, Fémfizika Intézet, UrB RAS, Jekatyerinburg;
Gottlieb B.M. Műszaki tudomány doktora. professzor, a Mechatronika tanszékvezetője FGBOU HPE "Ural Állami Közlekedési Egyetem", Jekatyerinburg.
Figyeljük figyelmünket a "Természettudományi Akadémia" kiadójában megjelent folyóiratokra,
(A RINC nagy hatású tényezője, a folyóiratok tárgya minden tudományos területet lefedi)
Tudományos folyóirat ISSN 1812-7339 | ПИ №77-63397
Technikai ügyfélszolgálat - [email protected]
Bizenkov M.N. folyóirat ügyvezető titkára - [email protected]
A folyóirat anyagai a Creative Commons licenc "Attribution" 4.0 World alatt állnak rendelkezésre.