Lineáris automatikus vezérlőrendszerek frekvencia jellemzőinek szintézise
SZÖVETSÁGI ÜGYNÖKSÉG AZ OROSZ FÖDERÁCIÓ OKTATÁSÁRA
RYAZAN ÁLLAMI RÁDIÓI MŰSZAKI EGYETEM
"A lineáris automatikus vezérlőrendszerek frekvencia-jellemzőinek szintézise"
Befejezett művészet. c. 511
logaritmikus frekvencia nyitott hurok
1. A nyitott rendszer logaritmikus frekvencia-jellemzőit a megadott minőségi mutatók szerint alakítsa ki.
2. Határozza meg a LAX és az LFH stabilitási tartalékait az erősítéssel és a fázissal.
3. Írja le a nyitott rendszer átviteli függvényét a megépített LAX-ra.
4. Számítsa ki és állítsa össze a zárt rendszer frekvenciaválaszát.
1. Állandó hiba: az idegesség (# 948, st / x0) · 10 2 = 0.5
2. A vágás gyakorisága: # 969; cp (2 + n) · 10 -2 = 3, ahol n = 1
3.Logaritmikus átviteli együttható L01 frekvencia 0,1 # 969, legalább 26 dB.
4. Stabilitás # 916; # 966; ± 10 0 = 40 0
5. A kötelező inerciális kapcsolatok állandó időtartama: Tin1 · 10 4 = 7, Tin2 · 10 5 = 3
6. A harmonikus interferencia gyakorisága (# 969; n / # 969; cp) · 10 -2 = 3
7. Az Lp interferencia-elnyomási tényező nem kevesebb, mint 80 dB
Nyílt rendszer LAX és LPC építése
A LAX megépítése alacsony frekvenciájú aszimptotával kezdődik. mert Statikus hiba van beállítva, a rendszer statikus lesz. A LAX lejtése az alacsony frekvenciájú aszimptotának nulla lesz, és a hibát a # 948; c = x0 / (1 + k).
k = x0 / # 948; ст -1 = 2 * 10 2 -1 = 199 a nyitott rendszer átviteli együtthatója
L1 = 20 lg (k) = 20 lg (199) = 46 a nyitott rendszer logaritmikus átviteli együtthatója
Ie az alacsonyfrekvenciás aszimptot m (1; 46) menti a frekvencia tengelyével párhuzamosan.
A szükséges fázisstabilitási határ biztosítása érdekében a LAX-nak meg kell haladnia a frekvencia tengelyt -20 dB / dec-os dőlésszöget a vágási frekvencián.
A LAX beépített szakaszai egyenes vonallal vannak összekötve -40 dB / dec-os lejtőn, míg az eredeti adatok 3. tételének kiválasztása érdekében # 969; c1 = 5pd / s, majd t (10; 26) (t. (0,1 # 969; cp; L01)) az egyenes vonal alá esik, nulla lejtéssel.
Konjugálási frekvencia # 969; c2 a stabilitási küszöb állapota fázisban van kiválasztva # 916; # 966; ± 10 0 = 40 0 (mivel a későbbi tipikus és kötelező inerciális kapcsolatok további fázist váltanak): # 969; c2 = # 969; cp / 2 = 50 rad / s.
Beépített LAA követően kialakult tipikus sorozat csatlakozó egységek: szabadonfutó k (p) = 199, két inerciális k (p) = 1 / (1 + T1 p) és a nyomásfokozó 2 k (p) = (1+ T2 p). így a tipikus linkek kapcsolódási funkciója így fog kinézni:
Az eredményül kapott átviteli függvény LFR-je az egyes kapcsolatok LFH hozzáadásával van kialakítva.
Az ábrából látható, hogy amikor egy tipikus vonalkötés van csatlakoztatva, a rendszer LPC-je nem esik egy előre meghatározott stabilitási tartományban a fázisban. Ennek a feltételnek a biztosítása érdekében további inerciális kapcsolatot kell létrehozni egy interfész frekvenciával # 969; c3 a vágási frekvencia felett. Egy további inerciális kapcsolattal rendelkező rendszer egy adott időközön belül áthalad # 969; c3 = 333 nap / s.
Dostraivalos LAA és LPC rendszer figyelembe veszi a megadott linkre kötelező inerciális egység 5. igénypont eredeti adatokat, és ellenőrizze, hogy visszaszorítja a harmonikus interferencia 6. és 7. kezdeti adatok:
Ábra azt mutatja, hogy a T (30 × 10 3; -80). LAA fölött fekszik nyílt hurkú rendszer, így az a követelmény, hogy a elnyomása harmonikus interferencia végezzük.
A stabilitási készletek meghatározása
Grafikusan rajzolunk egy nyitott rendszer LAX és LPC konstrukciójára.
A megerősítés stabilitása # 916; L = 24dB.
Fázis stabilitási tartalék # 916; # 966; = 45 0.
Nyitott rendszer átviteli függvényének rögzítése egy aszimptotikus LAX-hez képest
A 0-nál közeli frekvenciáknál a LAX nulla lejtéssel rendelkezik, ami azt jelenti, hogy a k (p) = k transzferfüggvénnyel létrehozott inerciális kapcsolatot képezi. A # 969, c1 változik a meredeksége - 40 dB / évtizedben - a lejtőn van látva két inerciális linkek k (p) = 1 / (1 + T 1 p) 2 T 1 = 1 / # 969; c1. Ilyen lejtőn a LAX megy # 969; c2. majd a meredekség -20 dB / dec értékkel egyenlő. A lejtés változtatását + 20 dB / dec értékkel a k (p) = (1 + T2 p), T2 = 1 / # 969; c2. A # 969; .. C3 lejtőn változtatásokat - 20 dB / évtizedben, és egyenlő a - 40 dB / évtizedben, azaz hat inerciális elem k (p) = 1 / (1 + T 3 p). A # 969; .. In1 lejtőn változtatásokat - 20 dB / évtizedben, és egyenlő a - 60 dB / évtizedben, azaz hat inerciális elem k (p) = 1 / (1 + p Tin1). A # 969; .. In2 lejtőn változtatásokat - 20 dB / évtizedben, és egyenlő a - 80 dB / évtizedben, azaz hat inerciális elem k (p) = 1 / (1 + p TUH2).
Egy LAX nyitott hurok konstrukciójában tipikus lineáris kapcsolatokat használtak, így a rendszer átviteli függvénye ilyen kapcsolatok halmazaként írható.
,
A független véletlen folyamatok generálása
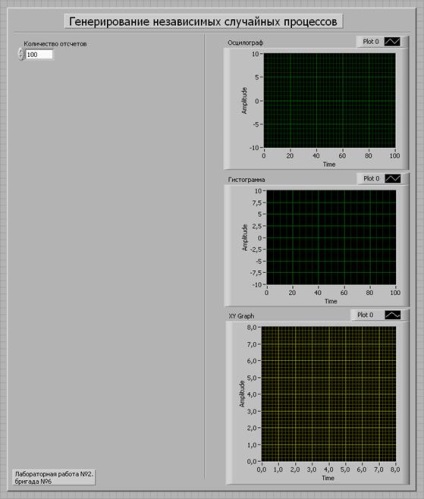
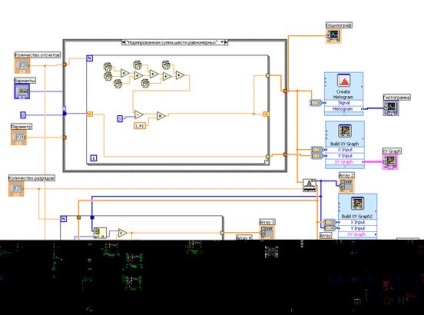
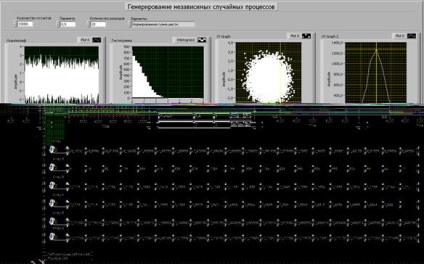
1. Az előlapot a laboratóriumi munka módszertani utasításainak megfelelően formálja.
Ezután a BlockDiagram ablakban adja hozzá a hiányzó elemeket: a ForLoop struktúrát, és hozzon létre egy hisztogramot. Ezután minden elemet megfelelő módon csatlakoztatunk. Állítsa be a számlálások számát 100-ra és futtassa a szimulációt.
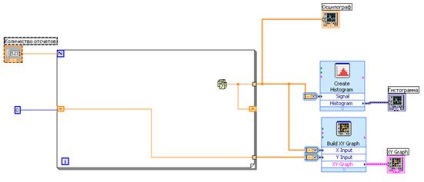
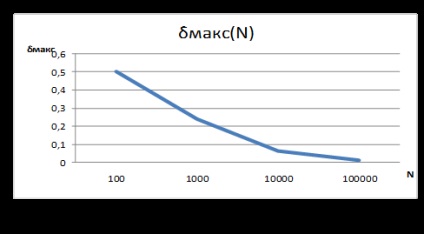
A különböző minták számának valószínűségének kiszámításához legnagyobb relatív hibát számítjuk ki N:
dmax = | 10 -15 | / 10 = 0,5
dmax = | 100 -124 | / 100 = 0,24
dmax = | 1000 -945 | / 1000 = 0,065
dmax = | 10000 -10129 / 10000 = 0,0129
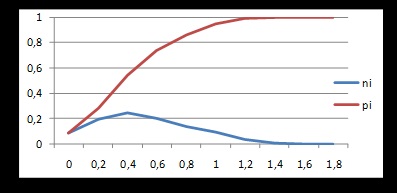
Úgy véljük, hogy az N (a kísérletek száma) és m (a számjegyek száma) a következő összefüggésben kell megtalálni:
Ez a kapcsolat azzal magyarázható, hogy amikor a számjegyek száma nő, szükség van a számlálások számának növelésére. Ellenkező esetben a terjesztés hisztogramja robusztus és nem teszi lehetővé számunkra, hogy jó pontossággal megítéljük a valószínűségi változók eloszlását.
2. Véletlenszerű sorrend létrehozása az egyenlőtlenségi rendszertől eltérő eloszlási törvénysel.
A ForLoop struktúrát másolták - egy egyenletesen elosztott véletlen sorrend generátora. Az opciók kapcsolójánál a "nemlineáris átalakítás" be van állítva. Az eredménytelen üres mezőben egy másolt ForLoop struktúrát helyezett be. A ForLoop struktúrán belül a program blokkvázlata az u = s (-2ln (1 - x)) 1/2 képlet segítségével generálódik.
Állítsa be a paraméter értékét a 0.5 változathoz és a számlálások számához - 1000.
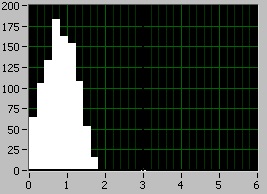
Elkezdtük a szimulációt. A függvény táblázatát a ni (x), pi (x),
3. Véletlen szekvenciák generálása egyenletesen elosztott véletlen szekvenciák hozzáadásával (az összehajtható véletlen változók száma 2-6.).
Adjunk hozzá még 6 variációt: "A két egyenruha összege", "Három egyenruha összege", "Négy egyenruha összege", "Öt egyenruha összege", "Hat egyenruha összege", "Hat egységes uniformizálás összege".
Minden egyes változat esetében a megfelelő sémákat összegyűjtjük az esetszerkezetben.
1) Két egyenlet összege:
2) Három egyenruha összege
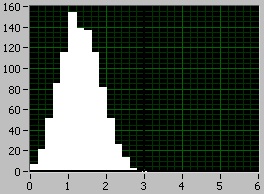
3) A négy egyenruha összege
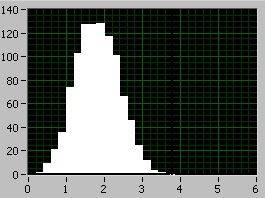
A kapott eredményeket azzal magyarázza, hogy a véletlen változók első és második pillanatai hozzáadódnak. Ie növekvő mennyiségű egy ideje vár szőnyeg növekszik 0,5 (az érték a szőnyeg. készenléti egységes véletlen változó tartományban 0-1) és despersiya is lépteti 1 (az érték a diszperzió egyforma random értéktartomány 0-1).
4. A hat egyenletesen elosztott véletlen változó normalizált összegének elosztási törvényének közelségének meghatározása a normális törvényhez.
A BlockDiagram és a FrontPanel ablakban új elemeket adunk hozzá a feladat megoldásához: