A funkciók minimalizálása - stadopedia
Először is meg kell tudnod írni az SDNF-et és az SKNF-et, mert ez valószínűleg a kontroll alatt áll. Mit lehet olvasni, és anyagokban, és más hozzáférhető forrásokban? Röviden, az SKNF egy tökéletesen konjunktív normális forma, és az SDNF egy teljesen diszjunktív normális forma.
Elég konjunktív NP - egy együttállása diszjunkcióban, és minden egyes diszjunkció (mindegyik konzol) tartalmazza az összes változót a képletben vagy a negáltja nem azonos diszjunkcióban, mindegyik diszjunkció nem azonos kifejezések:
Teljesen diszunktív NF - a kötőszövetek diszjunkciója. és minden kötőszóban vannak minden olyan változó, amely belép a képletbe, vagy negálódik, nincsenek azonos kötőszavak, minden kötőszóban nincsenek azonos kifejezések:
Most nézzünk egy példát, amelyben az igazságtábla segítségével SDNF-t és SKNF-et készítünk, majd folytatjuk a minimálisra csökkentését.
Például, vegyen egy függvényt három változóval, és már lefordította a leckét.
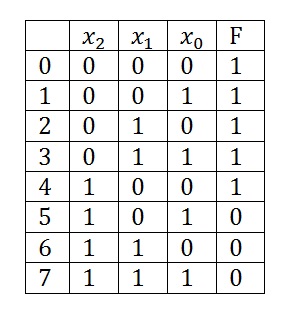
Tekintsük meg a CDNF összeállításának pontját:
1. Leírjuk a változókészletek termékét. ha a függvény 1 (F = 1);
2. Negatív változót veszünk, ha értéke 0
3. Egy változócsoport minden egyes terméke között a logikai kiegészítés jeleit tesszük
Most összeállítsuk a CDNF-et a mi igazságtáblánkra.
Tekintse meg az SKNF összeállításának pontjait:
1. Leírjuk a változókészletek termékét. ha a függvény 0 (F = 0);
2. Vegyen egy negatív változót, ha értéke 1;
3. Egy változócsoport minden egyes terméke között a logikai kiegészítés jeleit tesszük
Összeállítjuk az SKNF-et az igazságtáblázathoz.
Most lépjünk tovább a funkciók minimalizálása érdekében.
Először nézzük meg, hogyan egyszerűsítjük az SDNF-et és az SKNF-et. Kezdjük az SDNF-vel:
Most olyan párokra keresünk, amelyek csak egy változóban különböznek, azaz egy esetben negatív, a másik esetben pedig nincs. Az ilyen párokat választjuk (itt az ilyen párok ugyanolyan színeket kapnak):
De érdemes megjegyezni, hogy ha a szavakat párokra osztja, akkor az egyik szótag marad pár nélkül. És itt forduljunk a logika algebrai axiómáira: Ebből kiindulva a következő transzformációkat végezzük:
Most osztjuk meg a párokat, hogy illeszkedjünk, és ugyanazokat a változókat tegyük a zárójeleken kívülre, majd a zárójelek tartalmát lerövidítjük (hogyan és miért történik ez, tudnia kell):
Most lépjünk tovább az SKNF minimalizálása érdekében. Az elv ugyanaz, mint az SDNF esetében:
Valószínűleg az SDNF fölött lesz irányítanunk, de készen kell állnunk az SKNF-re is. És most pontosan mi lesz az ellenőrző szobában. A Carnot térképek egy másik módja a minimálisra csökkentése.
Már dolgozni fogunk az igazatáblával, amellyel rendelkezünk. Először a következő táblázatot vonjuk le:
Külön figyelmet kell fordítani a táblázat számozására. Emlékezned kell erre.
Most töltjük ki az asztalt. A megfelelő cellákat 1 töltjük fel, ha F = 1, és üresen hagyjuk, vagy 0-t állítunk be, ha F = 0:
Most keresse meg a szomszédos 1 csoportokat, amelyek hurkolnak. A közelben 1, vízszintesen és függőlegesen egymás mellett állva. Tehát a szomszédos extrém 1, azaz 1 a mutató sejtek 0 szomszédos sejtek 1. 2. Ha nehéz megérteni, hogy mit jelent a „tartási”, akkor ne feledje, hogy az a csoport egységei állhat 2, 4, 8, és bármely más online egységeket a n erejéig. És ezek a csoportok csak egy négyzetbe vagy egy téglalapba ragadhatnak. Szintén a különböző csoportok, ha szükséges, lehet, hogy egy és ugyanazon 1. A végén úgy vélem, hogy egy pár speciális esetekben, de most térjünk vissza a példát. Válassza ki a csoportokat:
A feketével kiválasztott csoport legyen az 1. csoport, és a piros csoportban kiemelt csoport 2. csoport. A változók változatlan csoportjait vizsgáljuk. Az 1. csoportban ez x2, és a 2. csoportban x1 és x0. Most megnézzük, milyen értékek ezeken a változókon: ha 0, egy negatív változót veszünk, ha 1, akkor nem. És kapjuk a következő egyenletet:
Most egy kicsit többet a Carnot térképéről. A vezérlő három és négy változójával fogunk működni, ezért itt van a négy változó táblája, amit fel kell jegyeznünk, különösen a számozásra.
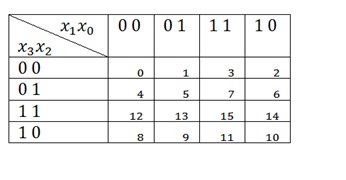
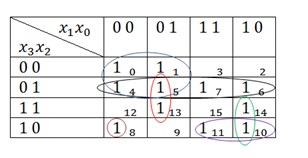
És most egy ilyen táblázatban további két, az 1:
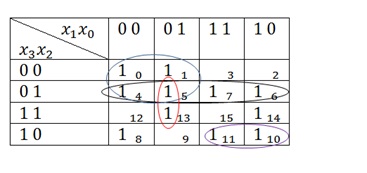
Itt szinte minden 1 csoportot rendelnek. A maradék sejteket csak 1 14. és 8. Először egy pillantást 1 a cellában 14. szomszédos egyik cella a 6. és 10. De ahogy usche tudja, hogy nem egy csoport három 1. Következésképpen lehetséges, hogy egyesítse a 1 csoportban 1 vagy a 6-os vagy a 10-es cellából. És ez, és ez igaz lesz. De nem kombinálhatod az 1-et és a 1-et a 6-os cellából és a 10-es cellából. Azaz:
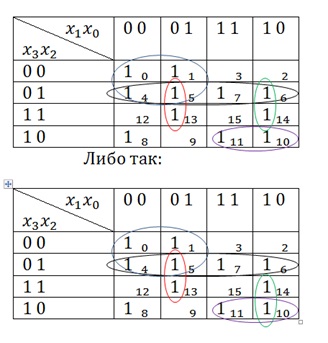
Maradt 1 a ketrecben 8. Ez minden egyszerű. Ha nincs olyan ember, akivel megjavítanák, akkor magára helyezi magát. Így fog kinézni:
Nos, mint minden. Lesz kérdése, kérjük, lépjen kapcsolatba. Sok szerencsét mindenkinek a kontrollon!