Keresse meg az online számológép négyzet alakú területét
Általános elmélet a tér négyzetének kiszámításához.
A négyzet egy rendszeres sík alak, amely négy pontból áll, amelyek közül három nem fekszik egy sorban, és négy szegmens, amelyek összekapcsolják a négy pontot, mindegyik oldaluk és szögeik egyenlőek.
A pontokat a négyzet csúcspontjainak nevezik, és tõke latin betûkkel jelölik.
A szegmenseket a négyzet oldalainak nevezik, és két nagybetűs latin betű jelöli azokat a csúcsokat, amelyek a szegmensekhez csatlakoznak.
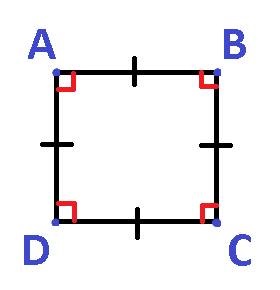
Az 1. ábrán látható az ABCD, A, B, C, D és oldal AB, BC, CD, DA csúcsa.
Az AB és az AD sugarak által alkotott szög az A csúcs szöge. A jelet ∠A vagy ∠BAD, vagy ∠DAB jelöli.
A BA és a BC sugarak által létrehozott szög a B csúcson van szögben. Ezt ∠B vagy ∠ABC vagy ∠CBA jelöli.
A CB és a CD sugárzás által létrehozott szög a C csúcson szög. Ezt ∠C vagy ∠DCB vagy ∠BCD jelöli.
Az AD és a CD sugárzás által létrehozott szög a D csúcson szög. Ezt ∠D vagy ∠ADC vagy ∠CDA jelöli.
Amint az a definícióból látható, a négyzet oldala egyenlő (AB = BC = CD = DA). A négyzet szögei szintén egymással egyenlők (∠A = ∠B = ∠C = ∠D) és 90 0.
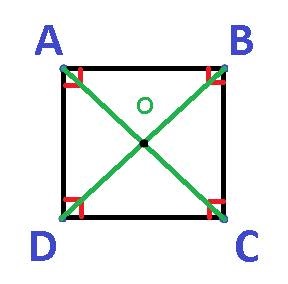
A 2. ábrán az AC és BD szegmenseket a négyzet átlói nevezik.
A négyzet átlói metszenek, és a metszéspont fele fel van osztva. Azaz AO = CO = BO = DO.
A négyzet átlói szétválasztják a szögeket, ahonnan félbehoznak.
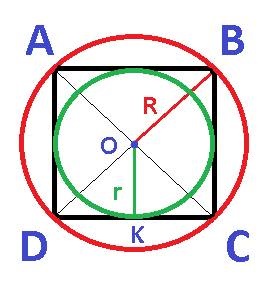
3. ábra: ABCD négyzet beírt és körülírt körrel.
A beírt és körkörös kör középpontja egybeesik és a négyzet átlóinak metszéspontjában fekszik.
A 3. ábrán az OK szegmens a körülírt kör sugara r, és a szegmens OB az R sugara, amely a kör négyzetének körül van írva.
Ha a négyzet oldalát az a jelű betű jelöli. átlós a d betűvel. akkor a következő kapcsolatok tartják:
1. A körülírt kör sugara r egyenlő a négyzet oldalának felével.
2. A kör négyzetével körülírt R sugár egyenlő a négyzet átlójának felével. Mivel a d négyszög átlója a kapcsolattal oldalra van kötve, nem nehéz elérni a kör négyzetével és oldalával körülírt sugár függését:
A sík alak S területe, amelyre a négyzet utal, egy határolt zárt tér a síkban. A lapos terület területe mutatja ezt a számot.
A terület számos tulajdonsággal rendelkezik:
1. Nem lehet negatív.
2. Adott egy bizonyos zárt térségben egy repülőgép, amelynek tagjai több darabból készül, amelyek nem metszik egymást (azaz a számok nincs közös belső pontja, de lehet, hogy viszonyulnak egymáshoz), akkor a területet egy ilyen régió négyzetösszege alkotó darabok .
3. Ha két szám azonos, akkor területük egyenlő.
4. A tér négyzet, amely egy egységnyi időközönként van kialakítva, egyenlő egyvel.
A mérési egység esetében a négyzetet úgy kell venni, mint a négyzet négyzetét, amelynek oldala megegyezik a szegmensek mérési egységével.
A problémák megoldásakor gyakran használják a négyzet alakú terület kiszámításához a következő képleteket:
1. A négyzet négyszöge megegyezik oldalának négyzetével:
2. A négyzet négyszöge megegyezik a diagonál négyzetének felével:
3. A négyzet négyzet négyszög az ívelt kör sugarával:
4. A négyzet négyszöge megegyezik a körkörös kör négy négyzet sugarával:
1. példa: Számítsa ki az a = 3 oldalsó négyzetet.
A négyzet négyzetének megtalálásához a tér területének kiszámítására szolgáló képletet használjuk:
Így az alábbiakkal rendelkezünk:
2. példa: Keresse meg az S = 144 cm 2 területű tér oldalait.
A tér oldalának megkereséséhez a négyzet négyzetének kiszámításához használjuk a képletet:
Az adott képletből a tér oldalát fejezzük ki:
Így az alábbiakkal rendelkezünk:
3. példa: Számítsa ki a négyzet négyzetét, amelynek átlója d = 6.
A négyzet négyzetének megtalálásához a tér területének kiszámítására szolgáló képletet használjuk:
Így az alábbiakkal rendelkezünk:
4. példa: Keresse meg az S = 32 cm 2 területű négyzet átlóját.
A négyzet átlójának megkereséséhez a négyzet négyzetének kiszámításához használjuk a képletet:
Ebből a képletből a négyzet átlója:
Így az alábbiakkal rendelkezünk:
5. példa: Számítsa ki a négyzetet, ha a benne írt kör sugara r = 5.
A négyzet négyzetének megtalálásához a négyzet négyzetét kiszámító képletet használjuk:
Így az alábbiakkal rendelkezünk:
6. példa: Keresse meg az ívelt kör sugarát, ha területe S = 225.
A körbe írt négyzet sugarának megtalálásához használjuk a tér területének kiszámítására szolgáló képletet:
Mutassuk meg az adott képletből egy négyzetbe írt kör sugarát:
Így az alábbiakkal rendelkezünk:
7. példa: Számítsa ki a négyzetet, ha a körülírt körkör sugara R = 7.
A négyzet négyzetének megtalálásához a tér területének kiszámítására szolgáló képletet használjuk:
Így az alábbiakkal rendelkezünk:
8. példa: Keresse meg a kör négyzetével körülírt sugarat, ha a területe S = 200.
A kör négyzetének közelében leírt sugarat a négyzet négyzetének kiszámításához használjuk:
Mutassuk meg az adott képletből a kör négyzetére leírt sugarat:
Így az alábbiakkal rendelkezünk: