A lecke témája a "geometriai alakok területe", a tartalom platform
Lecke témája: "A geometriai alakzatok tér"
Módszertani: tanulság építése a rendszer-tevékenység megközelítés szemszögéből;
Oktatás: a tudás ellenőrzése és rendszerezése a témában: "geometriai formák tér"; a problémák megoldásának elméleti és gyakorlati kérdések elsajátításának ellenőrzése, a tudás korrekciója;
Fejlődés: a kognitív aktivitás, a memória, a figyelem, a logikai gondolkodás, a matematikailag művelt beszéd; a független munka készségeinek kialakulása, az önértékelés készsége és a kölcsönös becslés, a csoportos munka készségei;
Oktatási: kommunikációs kultúra oktatása. állandó érdeklődés a matematika tanulmányozásához, a csoportos tevékenységek felelősségteljes és komoly hozzáállásához.
A tréning típusa: a tanulás lecke és a tudás rendszerezése.
A képzés típusa: tematikus.
A tanítás módszerei és módszerei: önálló munka és kiscsoportos munka.
Berendezés: kártyák, plakát.
A lecke felépítése:
2. A kísérleti tanulási tevékenység frissítése;
3. Az alapismeretek frissítése a témában: "Számok tér";
4. Orális munka;
5. A feladatok megoldása a rajzok szerint;
6. Gyakorlati munka "Builder" üzleti játék formájában;
Az elmélet konvergenciája a gyakorlatban a legkedvezőbb eredményeket hozza, és egyik gyakorlat sem hasznára válik, a tudományok önmagukban is kifejlődnek.
A tanár bevezető beszéde.
Jó napot, kedves gyerekek! Ülj le, kérlek. A nap valóban fantasztikus ma. Először is, hogy ma találkoztunk. Másodszor, érdekes dolgunk van. És harmadszor, új tudással gazdagodunk magunkat, mindkettőtök és én.
Ma szokatlan lecke van. Megpróbáljuk kombinálni az elméletet a gyakorlatba. És meg fogják győződni arról, hogy a geometria nem "száraz" a ponton, de a geometriai leckékben szerzett ismeretek hasznosak lehetnek a mindennapi életben. Ez már az ókor óta ismert. Az egyik ősi leírásban azt mondják, hogy Ptolemai király egyszer megkérdezte Euklidet, vajon van-e rövidebb és könnyebb út geometriája, mint a könyvei, amelyre azt válaszolta, hogy a geometriában nincsenek királyi utak.
Igen, a geometria egy magas spirál lépcső. Ebben teljesen együtt élnek, szigorúak, szépek és könnyedek.
2. A kísérleti tanulási tevékenység frissítése;
A lecke témája a "geometriai formák tér".
(Cél) Ma megtanuljuk, hogyan alkalmazzuk a képleteket a gyakorlati problémák megoldására, ezért:
Röviden megemlítjük a területek képletét, megoldunk több feladatot a rögzítéshez, gyakorlati munkát végezünk csoportokban.
Tehát ismételjük meg az előző tanórákon tanult képleteket.
3. Az alapismeretek naprakésszé tétele a témában: "Számok négyzetek"
A táblán egy sor számok, rajzok és képletek. A hallgatók összehasonlítják az ábrát és a képletet.
1. Problémák megoldása kész rajzokon.
A tábla a következő feladatokat látja el: rajzolás és állapot.
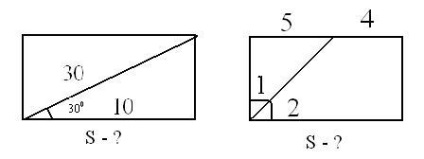
Kérjük, vegye figyelembe, hogy van egy kép és egy állapot a táblán. Olyan feladatokat kínálok fel, amelyekre szükséged van a figyelemtől, a leleményességtől, a minimális időtartamtól, de a legnagyobb lelkesedéstől. (450 és 45 négyzetméter)
2. Meg kell mutatni, hogy a témával kapcsolatos tudás gyakorlati jelentőséggel bír. Ehhez a hallgatókat arra kérik, hogy szóban válaszoljanak a kérdésre:
Melyik családnak van a legjobb életkörülménye? Ha a család Petrovyh, amely 3 főből áll, lakóterület 27m2. Családi Fedorovyh, áll 4 fő, foglal egy 48m2 lakás. (A Fedorovok)
5. A problémák megoldása a rajzok szerint.
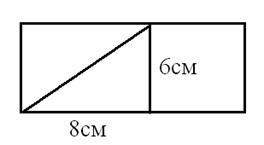
Mi a képen a kép? (Négyszögletű háromszög 6cm és 8cm lábakkal)
· Számítsa ki területét.
· Ki számította ki a pontszámot a táblára (a diák a képletet a táblán számolja).
· A háromszög kisebb oldalán rajzoljon egy négyzetet, és számítsa ki a területét. Írja az eredményt. (A diákok az eredményeket az S = 36 cm2-es számon belül írják le)
Milyen képet kaptál? (Trapéz, amely jobb háromszögből és négyzetből áll).
· Számítsa ki területét (kétféleképpen számítható ki: a képlet szerint vagy S = S1 + S2, S = 24 + 36 = 60cm2)
Ki fogja kiszámítani az első vagy második utat? Milyen következtetések vonhatók le? (Ha az ábra részekre van osztva, akkor ennek az értéknek a területe megegyezik a részei területének összegével).
Most vegye fel a trapézet a téglalapra és számítsa ki a területét. (A négyszögből és két egyenlő téglalap alakú háromszögből áll (egyenlő a hypotenuse és a láb). A négyszög területe a részterületek hozzáadásával vagy az S = ab.
· Kérem, vonjon le egy következtetést. (Ha az ábra részekre van osztva, akkor ennek az értéknek a területe megegyezik a részei területének összegével).
· Most pedig vegyük figyelembe a probléma megoldásának folyamatát.
· Kinek van bármilyen kérdése?
· Készültek, jól teljesítettek a feladattal.
6. Gyakorlati munka egy "Builder" üzleti játék formájában
Az építőipar ma a mechanikai folyamat, amely a gyárilag gyártott nagyméretű alkatrészekből álló épületek és szerkezetek összeszerelését jelenti. Az asztalos munka az építési és szerelési szervezetekben. faipari vállalatoknál, asztalos műhelyekben. Számos műveletet hajt végre a gépeken: körfűrészek - fűrészelt fűrészelés. gyalulással - gyalulással, fészkek hornyolásával és levágásával - fészkek kivágása és a tövisek levágása.
Ma építőként fogsz működni. Az építés alatt álló óvoda padlózatán végzett munka elvégzése szükséges. Javasoljuk, hogy a padlót egy 6,25 m X 8 m-es játékteremben alakítsák ki. A parketták négyszögletes háromszögek, parallelogramok és egyenletes trapéz alakúak. A csempe méretei centiméterben az ábrán láthatók. (64 - háromszög, 160 - trapéz, 160 - parallelogramm)
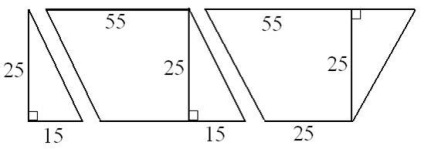
· A diákok 3 brigádra oszthatók.
· Az első csapat ácsok. A megadott méretű parkettákat olyan mennyiségben kell készíteni, hogy a padlóburkolatok után nem volt felesleges csempe, és a háromszög alakú lapok száma minimális volt, valamint a párhuzamos és trapéz alakú lapok - azonos összegűek.
· A második csapat a beszállítók. Meg kell adni a szükséges csempék számát az építkezés helyszínén. Ezt kiszámítják.
· A harmadik brigád parketta. A szállítmány ellenőrzéséhez előzetesen tudnia kell, hogy mennyi és milyen parkettacsempékre van szükség a padló fedezésére.
7. Az oktatási tevékenység reflexiója.
· Ideje összefoglalni a leckét.
· Nehéz volt a javasolt feladatok végrehajtásához?
• Érezted az elvtársak támogatását?
· Hol élnek az életetekben a tudás e témában?
· Mit szeretett a leckében?
Mit nem tetszett?