Többszörös adder gyorsított szállítással
3 kontúrt alakítottak ki. Két elem két kontúrja és négy elemének vázlata.
A szerkezeti képlet megírása az N-N alapjaiba a kettős negáció () és de Morgan törvény () törvényét használjuk.
A CS szerkezeti sémáját a NAND alapján az 1. ábrán mutatjuk be.
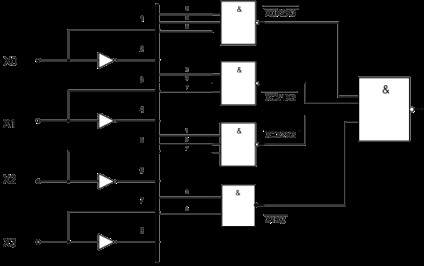
1. ábra. A CS szerkezeti sémája a NAND alapján
Többszörös adder gyorsított szállítással.
Az adder egy kombinációs logikai eszköz, amelyet számok aritmetikai adagolásának elvégzésére terveztek bináris kódban.
A gyorsított átviteli séma logikai séma a gyorsított átviteli jel kiszámításához. Alkalmazható az adagolóban gyorsított szállítással.
Általában a gyorsított átviteli sémák 4 számjegyű csoportra készülnek. A C1, C2, C3 és C4 szállítási jelek számítási ideje ugyanaz, és 3 * dt (1 * dt - a pi és gi jelek számítása és 2 * dt - az átviteli jelek kiszámítása). Ebben az esetben a 4 számjegyű csoport időtartama:
t4 = tc + ts = 3 * dt + 2 * dt = 5 * dt, ahol
tc a hordozó jel számítási ideje,
ts a modul összegzési számításának ideje.
A nagyobb bit kapacitású összeadóknál a 4 bites csoportok egymás után kapcsolódnak egymáshoz, és a második és a harmadik szint gyorsított szállításához kiegészítő rendszereket adnak hozzá.
1. a 64 bites adder-ben, csak az első szint gyorsított átvitelének sémáival, az addíció ideje:
t64 = 16 * t4 = 16 * 5 * dt = 90 * dt, az addíció gyorsulása 191/90 = 2,12-szer.
2. a 64 bites adderben a csak az első és a második szint gyorsított átvitelének sémáival az addíciós idő:
t64 = 3 * dt + 3 * dt * 4 + 3 * dt = 18 * dt, az addíció gyorsulása 191/15 = 10,61 alkalommal.
3. Az első, második és harmadik szint gyorsított átviteli sémáiban lévő 64 bites adderben az addíció ideje:
t64 = 3 * dt + 3 * dt + 3 * dt + 3 * dt = 12 * dt, az addíció gyorsulása 191/12 = 15,91 alkalommal.
A kapcsolási táblázat szerint általában az i-edik bit átadójelére a következő összefüggés áll:
3. táblázat: Átváltási táblázat
A gi, ri értékeket közbenső eredményeként és a teljes adder-ben számoljuk ki. Ezeknek a mennyiségeknek a jelentése egyszerűen megmagyarázható. A gi jel akkor jön létre, ha egy adott kisülésnél az átvitel az ai, bi bemeneti változók kombinációjának következménye. Ezért az úgynevezett átviteli generációs függvény. A Pi jel azt jelzi, hogy a Ci bemeneti jelet a legkevésbé szignifikáns bitben továbbítják. Ezért az úgynevezett átviteli terjedési funkció.
Az (1) kifejezés segítségével a következő képleteket lehet kiszámítani a közlekedési jelek kiszámításához:
Nyilvánvaló, hogy bár a kapott kifejezések meglehetősen bonyolultak, a segédfunkciók segítségével a továbbítási jelnek bármely bithez történő generálásának időtartamát csak a két elemen lévő jel terjedési késleltetési ideje határozza meg. Ezeket a funkciókat egy speciális kombinációs eszközzel valósítják meg - a gyorsított átvitel terve.
Az 1. ábrán. A 2. ábra egy négy számjegyű csoport párhuzamos átvitelére szolgáló eszköz vázlata. Ez a rendszer megvalósítja a (2) egyenletrendszert.
2. ábra A gyorsított átvitel terve
Az áramkör integrált változatban készül.
Több négy számjegyű számok hozzáadása több négyszélességű függesztő összekapcsolásával valósítható meg.
A rendszer és a működési elv
3. ábra Párhuzamos ADC
A bemeneti jelet a párhuzamosan csatlakoztatott komparátorok (DA1-DA8) inverz bemenetére táplálják. E komparátorok nem invertáló bemenetét az R1-R9 ellenállásoknál a feszültségosztó referenciafeszültségei látják el, minden összehasonlító esetében referencia töltést alkalmaznak, amely a kvantálási lépéstől eltér a szomszédosoktól. A mellékelt komparátorok száma bináris kódká konvertálódik a DD1 elsődleges jeladó használatával
· Nagy sebesség, elérve tíz nanoszekundumot.
· Nagy komplexitás (az áramkörben lévő komparátorok száma megegyezik a kvantálási szintek számával, és egyenlő 2n-val, ahol n a kimeneti kód bitmélysége
· Magas költségek - a magas költségek miatt;
· Ennek következtében az alacsony pontosság (8-10 bit)