induktor
A munka célja egy tekercs önindukciós tényezőjének meghatározása a teljes elektromos ellenállás (impedancia) mérésével váltakozó és egyenáramban.
Eszközök és berendezések: induktív (L), változó ellenállás (Rper.), Állandó áramforrás (# 949;), milliaméter AC és DC (mA), AC voltmérő
V), egyenáramú voltmérő (= V), elektromos oszcilláció (MH) generátor, egyenáramú forrás (# 949;).
Az elektromos áramlatokat és állandó mágneseket körülvevő térben egy mágneses mezőnek nevezett erőtér van. A jelenlétét a bevezetett vezetékeken vagy permanens mágneseken fellépő erő érzékeli.
Amper találta meg a hatalom. amellyel a mágneses mező a vezetőelemen a mágneses indukcióval közvetlenül az áram I-rel és az elem vektortermékével közvetlenül egyenlő árammal hat,
Az Ampère erőmodulját a képlet adja meg
hol van a szög a vektorok és; és.
Így a mágneses indukció vektora a mágneses mező erőssége. Ez utóbbit a mágneses indukciós vonalak képviselik, amelyek vonalai érintkeznek, és amelyek mindegyik pontban egybeesnek a vektor irányával. A mágneses indukciós vonal érintkezési pontja mentén helyezkedik el mágneses tűvel, az északi N vége pedig a vektor irányát mutatja.
Az Ampere törvény lehetővé teszi számunkra, hogy meghatározzuk a mágneses indukció mértékegységét. Hagyja, hogy az erősségű vezetőelem merőleges legyen a homogén mező mágneses indukciójára. Ezután az Ampère erő modulusa
at = π / 2 és a bűn = 1.
A mágneses indukció mérési egysége Tesla (T).
1 A Tesla a homogén mező mágneses indukciója, amely egy mágneses indukcióra merőleges egyenes vonalvezető hossza méterben egy méteres erővel hat, ha egy áram folyik ezen 1A vezetéken:
A mágneses indukció (mágneses fluxus) vektora a dS területen keresztül egy skála fizikai mennyisége egyenlő
ahol Bn = Bcos a vektor vetülete a normalizált dS egység vektorának irányára; a vektorok közötti szög; egy olyan vektor, amelynek modulusa dS (), és az irány egybeesik a dS helyének normális irányával (1.
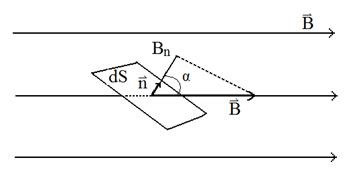
Egy homogén mező és a vektorra merőleges síkfelület esetén,
Bn = B = const és Ф = BS.
Az utolsó képletből meghatározzuk a mágneses fluxus Weber (Bb) mérési egységet.
1 Weber egy mágneses fluxus, amely 1 m 2 -es felület sík felületén halad át egy olyan homogén mező mágneses indukciójára, amelynek indukciója 1 Tesle:
Gauss tétele egy mágneses mező számára: a mágneses indukció vektorának fluxusa bármely zárt felületen nulla, azaz
Ez a tétel tükrözi a mágneses töltések hiányát, aminek következtében a mágneses indukciós vonalaknak sem eleje, sem végük nincsenek zárva.
A környező térben zárt áramkör mentén áramló elektromos áram létrehoz egy mágneses mezőt, amelynek indukálása a Bio-Savart-Laplace törvény szerint közvetlenül arányos a jelenlegi erősséggel. Ezért a mágneses fluxus Ф arányos az áramkör I áramkörével:
ahol L az önindukció együtthatója vagy az áramkör induktivitása. Ebből a kifejezésből meghatározható az induktivitás mérési egysége - Henry (HH).
1 Henry egy ilyen áramkör induktivitása, az önindukció mágneses fluxusa az 1A áramerőssége szerint 1 Weber:
Faraday felfedezte a törvényt: amikor a mágneses fluxus áthatol a felületen, amely a zárt vezetőkörön átnyúlik, megváltozik, az utolsó az indukció elektromotoros erejét (EMF) jeleníti meg:
A képlet mínusz jele a Lenz szabály matematikai kifejezése: az áramkör indukciós áramának mindig olyan iránya van, amelyben az általa létrehozott mágneses mező meggátolja a mágneses fluxus megváltozását.
Így, ahogy az áramerősség változik az áramkörben, a mágneses fluxus is hozzá van kötve, következésképpen az EMF indukálódik.
Az EMF megjelenése a vezető áramkörben, amikor az áramot megváltoztatják, önindukciónak nevezzük.
Ha Faraday törvényét önindukcióra alkalmazzuk, úgy találjuk, hogy az önindukciós emf
Ha a kontúr nem deformálódik, akkor L = const és
Ezért a tekercs végein az öninduktancia EMF van, amely megakadályozza az áramváltást.
Az önindukciós együttható meghatározása
Tekintsünk egy L induktorból álló elektromos áramkört. A tekercs aktív (ohmikus) ellenállást és induktív (reaktív) ellenállást # 969; L, ahol # 969; - a váltóáram ciklikus frekvenciája; L - tekercs induktivitás. Feltételezzük, hogy a tekercs ohmos ellenállása az R ellenállásban koncentrálódik, sorba kapcsolva (2. Az 1. és 2. érintkezők váltakozó feszültséggel vannak ellátva
U ciklikus frekvenciával # 969;
Legyen az első kapcsolat potenciálja # 966; 1 további potenciál a második kapcsolatról # 966; Aztán a jelenlegi balról jobbra haladok.
Tegyük fel, hogy a jelenlegi I növekszik, azaz.
Ezután a Faraday-törvény szerint az L-tekercs végein egy önindukciójú emf jelenik meg, amelynek iránya ellentétes az áramkör I áramának irányával:
Ha a bemeneti feszültség
U a harmonikus törvény szerint változik
ahol Um a feszültség amplitúdója.
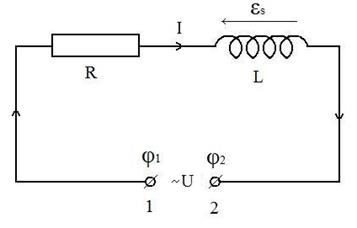
Ohm törvényét írjuk le a lánc ezen inhomogén szakaszára:
A differenciál-egyenlet (2) konkrét megoldása formában van
ahol Im az aktuális amplitúdó, az aktuális oszcilláció kezdeti fázisa.
Találjuk meg az első származékot:
A (7.3) és (7.4) kifejezések a (7.2) képletben helyettesíthetők:
Az egyenlőség (7.8) minden esetben megtartja az állapotot # 947; - # 946; = 0 és # 947; = # 946;. Ezután a (8) -ból megkapjuk
A (9) bekezdésből következik
az áramkörszakasz teljes elektromos ellenállása (impedancia), amely magában foglalja az aktív R ellenállást és az induktív ellenállást # 969; L tekercs induktivitás.
A gyakorlatban, egy voltmérő és egy ampermérő segítségével, a változó feszültségek és az aktuális amplitúdók hatásos (működő) értékeit az amplitúdókhoz viszonyítva mértük az alábbiak szerint:
A (10) kifejezéstől kapjuk
(# 969; L) 2 = Z2-R2
Ezért az induktor Z teljes villamos ellenállását egy váltakozó árammal és R állandó Ohmos ellenállásával mérve meg lehet találni a tekercs L induktivitását.
A munka teljesítményének sorrendje
1. Szerelje össze a működési áramkört az induktor teljes elektromos ellenállásának Z (impedancia) meghatározására váltakozó áramon (3.
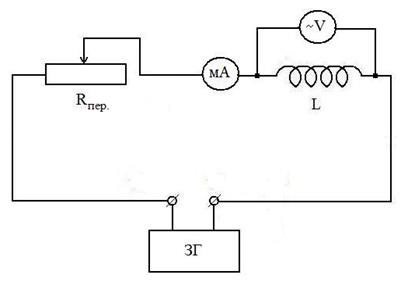
2. Állítsa be a változó ellenállás Rper maximális értékét. .
3. Kapcsolja be az MZ generátort.
4. Az Rper ellenállásának megváltoztatásával kapjuk meg az Ieff aktuális intenzitás öt értékét, és mérjük meg az induktív Ueff feszültségeket.
5. Az 1. táblázatban rögzítse a mérési eredményeket.
11. Számítsa ki az induktor R ohmos ellenállását és keresse meg az Rcp középértékét. .
gyakorisággal # 957; = 1000 Hz határozza meg az L-tekercs önindukciós tényezőjét.
1.Milyen mágneses mező? Mi a mágneses mező indukciós vonal?
2. Hogyan alakul az Ampere törvénye? A mágneses mező indukciójának mértékegysége.
3. Határozza meg a mágneses indukció vektorának fluxusát. A mérés egysége.
4. Mi a hurok induktivitás? A mérés egysége.
5. Formálja a Faraday-törvényt és a Lenz-szabályt.
6. Mi az önindukció jelensége? ED önindukciós tekercs.
7. A kölcsönös indukció jelensége. A jelenség gyakorlati alkalmazása.
8. Írja be a Maxwell egyenleteket integrált formában.
9. Az impedancia (impedancia) és az induktivitás öninduktivitásának kiszámítására szolgáló munkamódszereket dolgozzon ki.