A skaláris argumentum vektorfüggvénye, a függvény hodográf vektora

Definíció. Ha a paraméterek minden egyes értékéhez egy adott intervallumon belül egy meghatározott vektor (attól függően) felel meg, akkor a vektort vektorfüggvénynek (röviden vektorfüggvénynek) nevezik egy skaláris argumentumból, és ebben az esetben írj:

Amikor megváltozik az argumentum, a vektor mind nagyságban, mind irányban változik. Az alábbiakban azt feltételezzük, hogy egy intervallumban változik, véges vagy végtelen.

Feltételezzük, hogy a vektor a származásból származik, Egy pont sugárvektorja. Ebben az esetben, ha a paraméter megváltozik, a vektor vége a vonalat írja le. egy vektorfüggvény hodográfjának nevezik. A koordináták eredetét hodográf pólushoz nevezik. Az (1.1) egyenletet a görbe vektoregyenletének nevezik (1.1. Ábra).

Ha a vektor csak a modult változtatja meg, akkor az utazási idő görbe egy pólusból származó sugár lesz. Ha egy vektor modulusa állandó és csak az iránya változik, akkor a hodográf olyan vonal, amely egy gömbön fekszik, amelynek középpontja a pólusnak, és sugara egyenlő a vektor modulusával.

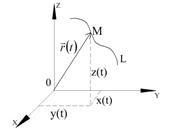
Ha egy téglalap alakú Descartes-koordinátarendszer tengelyein a vektor projections-jét jelöljük a térben, akkor ezek az értékek minden egyes paraméterértékre soron bizonyos számértékeket adnak és ezért a skaláris argumentum skaláris függvényei:

Így a skaláris argumentum vektorfüggvénye megegyezik azzal, hogy ugyanazt az argumentum három skaláris függvényét adja meg. mert az (1.1) egyenlet egy ív görbének egyenlete, akkor ugyanazt a görbét az (1.2) egyenlet adja. Az egyenletek (1.2) a térbeli görbe szokásos paraméteres egyenletei.