Nyomáserő a lapos és ívelt felületeken
A sík falon lévő hidrosztatikus nyomás ereje megegyezik a nedvesített sík fal tömegének közepén a nyomás szorzatával szorozva az S
ahol hc a sík fal súlypontjának merítési mélysége, m.
A lapos falon fellépő erő alkalmazásának koordinátája
ahol Jo a síkszerkezetnek a központi tengelyhez viszonyított tehetetlenségi nyomatéka.
Az ívelt felületen a nyomóerő a következő:
.
- hajlított felület vetülete függőleges síkra.
hol van a nyomó test térfogata, amelyet felülről a szabad felület síkja határol, az oldalakon a függőleges kiálló felület alulról az ívelt felületen.
Amikor problémákat old meg ebben a témában:
- az első szakaszban meghatározza az eredményes erő értékét;
- a második szakaszban határozza meg az erő alkalmazásának pontját és irányát.
Abban az esetben, ha legalább a vizsgált felület egyik oldalán a folyadék szabad felülete feletti nyomás különbözik a légköri felülettől, akkor a számítások során a szóban forgó felület gravitációs középpontjában lévő teljes hidrosztatikus nyomást kell használni.
Példa 1. Az L 'B = 3'4 m méretű téglalap alakú lengőlap zárja a gát kimenetét (2.2. Ábra). A bal oldalon a vízszint H2 = 2 m, a jobb oldalon - H1 = 5 m. Határozza meg a szükséges T húzóerőt az árnyékolás a szögben a horizonton való megnyitásához és a Fa erőhöz. amellyel az árnyékolást az A küszöbértékhez nyomják.
A megoldás. Határozza meg a pajzs bal oldalán ható erőt.
A nedvesített felület területe: m 2.
A súlypont merülésének mélysége: m.
Nyomáserő: kN.
A pajzsfelület jobb oldali nedvességtartalma: m 2.
A súlypont merülésének mélysége: m.
Ebben a témában meg kell érteni, hogy a Bernoulli-egyenlet az áramlás mechanikai energiájának megőrzésének egyenlete, amely egy kilogramm folyadék tömegre vonatkoztatva és az összehasonlítás közös síkjához viszonyítva határozható meg.
Az egyenlet bal oldalán az áramlás mechanikai energiája mindig nagyobb, mint az egyenlet jobb oldalán a v veszteség összege.
A folyadék mozgását az 1. szakaszból a 2. részbe a Bernoulli-egyenlet a következő formában határozza meg:
itt Z1. Z2 - geometriai fej, amely egyenlő az áramlás élő részével az összehasonlítás síkjáig tartó távolsággal;
. - piezometrikus fej, amely megfelel a piezométer leolvasásának a kiválasztott szakaszban.
Megjegyzés: Az egyenletben helyettesített nyomásértéket egy nyomásszintről kell leolvasni. Vagy mindkettő redundáns, vagy mindkettő abszolút.
. - nagysebességű fej, amely figyelembe veszi az áramlás kinetikus energiáját.
a1. a2 - Cariolis együtthatókat, figyelembe véve az áramlás aktuális kinetikus energiájának az energiához viszonyított arányát, az átlagos áramlási sebességből számítva.
A lamináris rezsim esetében a = 2. A turbulens a = 1,03-1,18.
- mechanikai energiaveszteség a folyadékmozgás során. Figyelembe kell venni azt a tényt, hogy amikor az ideális folyadék mozog, a fejveszteség 0. Minden egyéb esetben azokat összegnek kell tekinteni. ahol
- Súrlódási veszteségek. (2.10)
- a helyi ellenállások veszteségei. (2.11)
Az összehasonlító sík helyzetét úgy kell megválasztani, hogy csökkentsük az ismeretlen számok számát a Bernoulli-egyenletben.
Az egyenletet formában (2.9.) Írják, majd az összehasonlító sík helyzetét és a keresztmetszetek koordinátáit figyelembe véve, egyszerűsített formában írják le, míg az elhanyagolt kifejezéseknek indokoltaknak kell lenniük.
A sebességfej meghatározásához minden szakaszban szükség van a folytonosság egyenletére (az áramlás állandósága a csatornában)
A hallgató önállóan ellenőrzi a teljes és a piezometrikus fej vonalainak megépítését meghatározott adatokkal, figyelembe véve az adatokat. Például a tartályban lévő folyadék szabad felületén lévő teljes fejes vonal egybeesik a piezometrikus fej sorával, mivel V = 0.
Ha a szabad felület fölötti nyomás nagyobb, mint a légköri nyomás, a teljes nyomóvezeték áthalad a folyadékszint fölött stb.
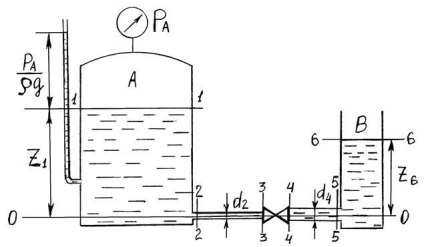
Egy példa. A különböző átmérőjű mm-es és mm-es csövekből álló csővezeték összekapcsolja az A vevőt a B légköri tartállyal. A vevőkészülék folyadékszintje m, a folyadékfelszín feletti nyomás. Határozza meg a B tartályban lévő szintet Q 1 folyadékáramlási sebesség mellett, amely 1 l / s. A fej veszteségei: a csővezeték kimeneti nyílásánál m; az első szakaszban h3 = 2 m; a csővezetéket elválasztó szeleppel, h4 = 2 m; a második szakaszban h5 = 5 m (2.4. ábra).
A megoldás. Válasszuk ki a csővezeték tengelyén áthaladó összehasonlító síkot, írjuk le a Bernoulli-egyenletet a két szekcióban, amely a szabad szinteken halad át az 1-1 vevőben és a 6-6 atmoszferikus tartályban.
hol van a teljes fejvesztés az 1-1-től a 6-6. szakaszig.
. A sebességet minden részre kiszámítjuk. Reynolds szám. a Kariolis-együttható meg van adva.