WolframAlpha orosz interpolációs függvények wolfram, alfa
Interpoláció - egyfajta közelítés. Azonban, ellentétben a közelítés a legkisebb négyzetek módszerével, ami a függvény egyenlete az ábrán húzódó legalább távolságra mindegyik pontot, interpoláció feladata, hogy megtalálja az egyenlet a funkció, a menetrend szerint halad pontosan minden adott pontot.
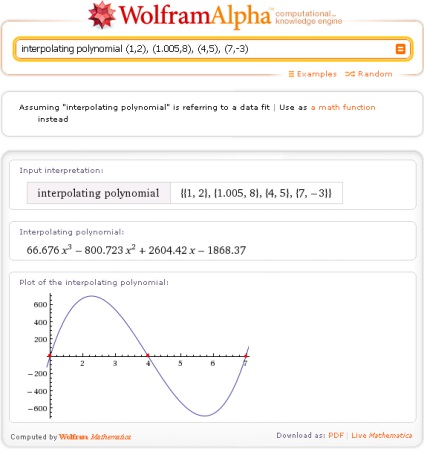
Vannak különböző interpolációs. Wolfram | Alpha használ polinom-interpoláció és végrehajtja azt kérésre Interpoláló polinom
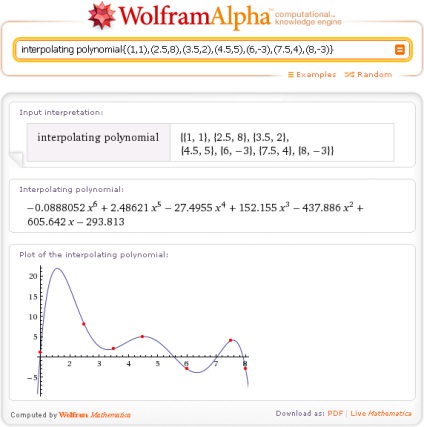
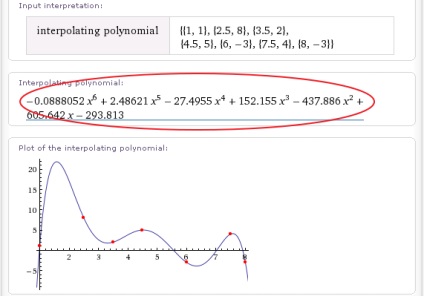
Válaszul a Wolfram | Alpha ad (b) egy sor adatot ez a kifejezés, mint ha kézzel beírja:
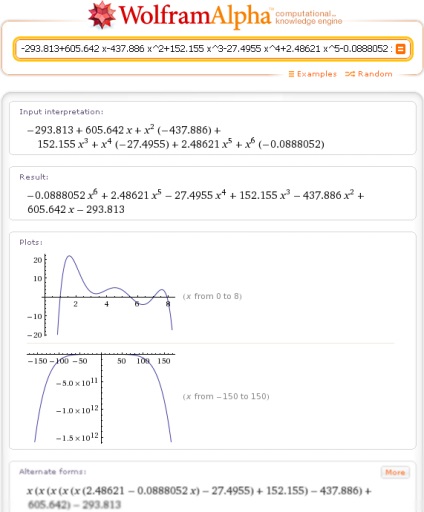
Végül (c) értékének kiszámításához az interpolációs polinom egy adott ponton (x = 4), csak meg kell adnia az ablak lekérdezés Wolfram | Alpha, miután a megadott polinom vesszővel elválasztott az érvelés, hogy ezt:

Közelítést ugyanazokat a pontokat, ha nem adsz meg semmilyen típusú bármilyen sorrendben közelítése modell, meghozta a következő:
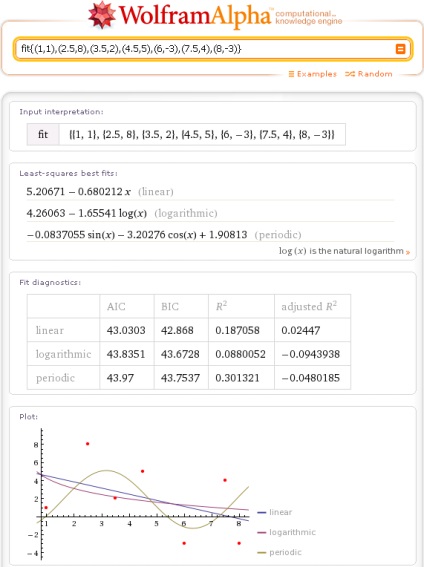
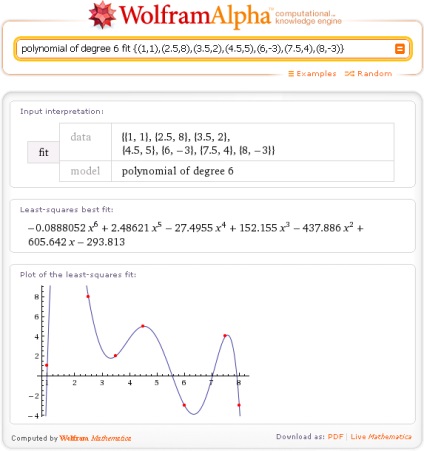
Tudod kap az eredmény a közelítés, amely egybeesik az eredmény a polinom-interpoláció. Ehhez válassza ki a polinom modell és határozza meg annak érdekében, 1 kisebb, mint a adatpontok száma:
Elvégzésére interpoláció fontos, hogy adott abszcissza pont nem esik egybe. Például itt van egy kérés (ez a baj!)
ahol az első és a második pont ugyanolyan abszcissza ad az eredmény első pillantásra kézenfekvő, de ez teljesen téves:
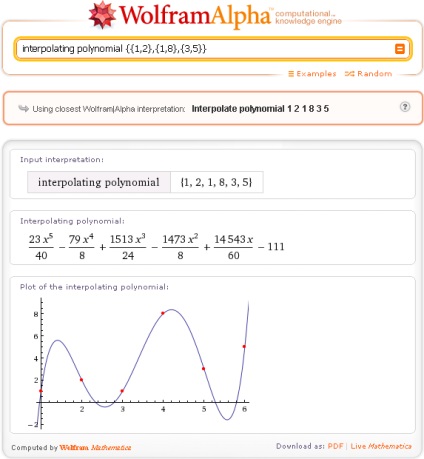
Itt is, mint látható, Wolfram | Alpha értelmezi a koordinátáit egy 3 pontos adatok sorozataként 6 szám - a függvény értékei, és használja az x szám a tagok ezt a sorozatot.
Ha az abszcissza az összes pontot egy kicsit, de ez más, kapsz teljesen korrekt eredményt (ez így van!):