generációs kombinációk

A kombinatorikus kombinációja N különböző elemeinek M M egy sor elemek közül kiválasztott N számú elemek. Ezek a készletek csak annyiban különbözik bekerülni őket bizonyos elemeit M, a sorrendben az elemek a készletben nem fontos. Készletek, különböző csak a sorrendben az elemek (de nem a személyzet) tartják ugyanaz, és ez a kombináció eltérnek elhelyezések.
Kombinációk ismétlések nélkül
Feladat. Találd meg az összes lehetséges kombináció nélkül ismétlése elemek sokaságát 2.
Vannak a következő kombinációkban:
A lehetséges kombinációk számának ismétlés nélküli N elemei M lehet meghatározni a következő képlet szerint (N≥M):
hogy M! szer kevesebb, mint a megfelelő számú elhelyezések ismétlések nélkül (anélkül ismétlődésüknél kombinációk nem függ a sorrendjét elemek).
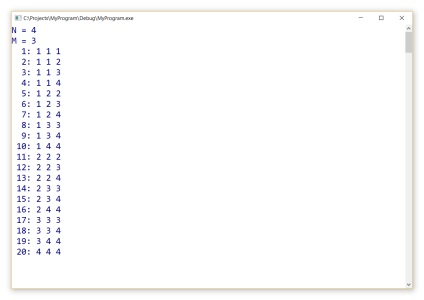
Tekintsük a problémát, hogy elérjük az összes kombinációk számok 1. N M.
Végrehajtása C ++
#include
using namespace std;
bool NextSet (int * a, int n, int m)
int k = m;
A (int i = K - 1; i> = 0; J)
ha (a [i]
A (int j = i + 1, j
return true;
>
return false;
>
void Print (int * a, int n)
static int num = 1;
cout.width (3);
cout <
int main ()
int n, m, * a;
cout <<"N = " ;
cin >> N;
cout <<"M = " ;
cin >> m;
a = new int [n];
A (int i = 0; i
Nyomtatás (a, m);
ha (n> = m)
míg a (NextSet (a, n, m))
Nyomtatás (a, m);
>
cin.get (); cin.get ();
vissza 0;
>
Kombinációk ismétlés
Kombinációk ismétlések nevezett m jelkészlet elemeit, ha minden egyes eleme a N készlet részt vehet többször. Ahol az arány értékeinek M és N nincsenek korlátozások, és az összes kombinációk ismétlésben
Egy példa erre a problémára a választás M képeslapok N minden lehetséges módon.
A generál kombinációk ismétlések az oldatot használjuk a generációs elhelyezések ismétlések szó ebben a cikkben.
Végrehajtása C ++
#include
using namespace std;
bool NextSet (int * a, int n, int m)
int J = m - 1;
míg (a [j] == N j> = 0) j--;
if (j <0) return false;
ha (a [J]> = n)
j--;
a [j] ++;
if (j == m - 1) return true;
A (int k = j + 1; k
return true;
>
void Print (int * a, int n)
static int num = 1;
cout.width (3);
cout <
int main ()
int n, m, * a;
cout <<"N = " ;
cin >> N;
cout <<"M = " ;
cin >> m;
int h = n> m. n. m; // a tömb mérete van kiválasztva, mint a max (n, m)
a = new int [h];
A (int i = 0; i
Nyomtatás (a, m);
míg a (NextSet (a, n, m))
Nyomtatás (a, m);
cin.get (); cin.get ();
vissza 0;
>
Az eredmény a fenti algoritmus: