bináris fák
// Ha igen, hogy a növekmény száma
if (t-> Bal () == NULL t-> Jobb () == NULL)
Mélység függvény fordított átviteli kiszámításának módszerét a mélység egy bináris fa. A mélysége az egyes csomópontok kiszámítjuk annak bal és jobb részfákat. Összesen mélység eggyel nagyobb, mint a maximális mélysége részfák.
// Ez a funkció a fordított módszer áthaladás
// számítani a mélysége a bal és a jobb részfa
// csomópont és visszatér az eredmény értékét a mélység,
// egyenlő 1 + max (depthLeft, depthRight).
// Mélység üres fa -1
sablon
void Mélység (TreeNode
int depthLeft, depthRight, depthval;
depthval = 1 + (depthLeft> depthRight depthLeft depthRight.);
b = GetTreeNode ( 'B', NULL, d);
c = GetTreeNode ( 'C', e, NULL);
a = GetTreeNode ( 'A', B, C);
Először létrehozunk egy fia D, amelyet ezután csatlakozik a szülő B, amikor létrehoz egy csomópontot. Alkotó csomópont E és C csatlakozik a szülei a születési időt (vagy teremtés) az utóbbi. Végül, létrehoz egy gyökér, és csatlakozik az ő fiai a B és C
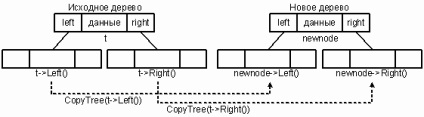
Fa algoritmus másolás kezdődik a gyökér és elsősorban konstrukciók bal részfa a csomópontra, majd - a jobb részfa. Csak azután, hogy egy új csomópont. Ugyanez a rekurzív folyamat ismétlődik minden egyes csomóponthoz. Ennek megfelelően, a csomópont a forrás fa t hoz létre egy új csomópont mutatók és newlptr newrptr.
Az ellenkező átviteli eljárás Sons látogatott, mielőtt szüleik. Ennek eredményeképpen egy új fát hoz létre részfák megfelelő T-> Bal () és a t-> Jobb (). Sons csatlakozzon szüleik idején létrehozása az utóbbi.
// létrehozni szülő, és csatolja hozzá az ő fiai
newnode = GetTreeNode (t-> adatok, newlptr, newrptr);
A lényege a látogató csomópont t a forrásfába teremt egy új csomópont a fa-két példányban.
TreeNode
MakeCharTree (root1, 0); // root1 jelzi Tree_0
Pass leszármazottai egy csomópont egy, a bal oldali részfa (B csomópont, majd a D csomópontot, amely egy jobb részfáját B csomópont). Hozzon létre egy új csomópont adatokkal megegyező D, a bal és a jobb mutatókat egyenlő NULL.
Node B telt fia. Hozzon létre egy új csomópont adatai megegyeznek a B, a bal index egyenlő NULL, a jobb mutatót a másolatot a csomópont D.
Mivel csomópont bal részfa elkészült, kezdjük a jobb részfa folyosón, és eléri a csomópont E. hozzon létre egy új csomópont az adatokat a csomópont E és a mutató területeken egyenlő NULL.
A feldolgozás után, E megy a szüleinek, hogy hozzon létre egy új site adataival C. A jobb mezőben, hogy a mutató NULL, és a bal mutató rendelhet linket egy példányát a gyermek csomópont E.
// Létrehozunk egy példányban a fa t, és visszatér a gyökere egy új fát
sablon
// Változó newnode jelzi az új csomópont jön létre
// keresztül Hívás GetTreeNode illeszthetők és
// a jövőben az új fa.
// csomópont és paraméterként adja át GetTreeNode
TreeNode
// megállítani az áramlást, ha a rekurzív
// csomópontja t. minden egyes csomópontnál a fa funkció
// Létrehozunk egy másolatot. Különben visszaküldi
// és leteszi őt fia.
if (t-> Bal ()! = NULL)
if (t-> Jobb ()! = NULL)
// egy új fa alulról felfelé, ami az első
// két fia, majd a szülő
newnode = GetTreeNode (t-> adatok, newlptr, newrptr);
// visszatér egy pointert az újonnan létrehozott fa
Amikor egy alkalmazás egy dinamikus struktúra, mint a fa, felelős a felszabadulás memória esik a programozó. Mi fejlesztjük a funkció DeleteTree, amely felhasználja a fordított módszer elhaladó bináris fa. Az eljárás befejezése fordított biztosítja, hogy meglátogatjuk a fiai szülőwebhely mielőtt kiveszed. Operation látogatás hívni FreeTreeNode függvény eltávolítja a csomópontot.
// A fordított algoritmust áthaladását facsomópontok
// és törli az összes csomóponton látogatása
sablon
void DeleteTree (TreeNode
ClearTree is kidolgozott, hogy a funkció törli az összes fa csomópontjait, és visszaállítja a gyökér. DeleteTree függvény meghívja az eltávolítása facsomópontok és hozzárendeli egy mutatót a gyökér érték NULL.
// Hívjon DeleteTree függvény eltávolítja a fát.
Ezután // vissza mutatót a gyökér a NULL
sablon
érvényteleníti ClearTree (TreeNode
t = NULL; // most a gyökér üres
Bináris keresés fák
A szokásos bináris fa tartalmazhat egy nagy adatgyűjtés, és még mindig a gyors kereső, add, vagy törölhet elemeket. Az egyik legfontosabb alkalmazása a fák, hogy létrejöjjön egy gyűjtemény osztályok. Lineáris szerkezetek bonyolultsága az algoritmust, amely megvalósítja a szekvenciális keresés O (N), amely hatékony nagy gyűjtemények. Általában a fa szerkezetek sokkal jobb teljesítményt, mint az út, hogy egy adott fa nem haladja meg a mélységet. keresés a hatékonyság maximuma az elkészült és bináris fa O (log2 N). Például a listán 10.000 tagja várható összehasonlítások számának szekvenciális keresés 5000. Keresés a kész fa lenne szükség legfeljebb 14 összehasonlításokat. Bináris fa számos lehetőséget hordoz magában, mint egy listát a tárolási szerkezet.
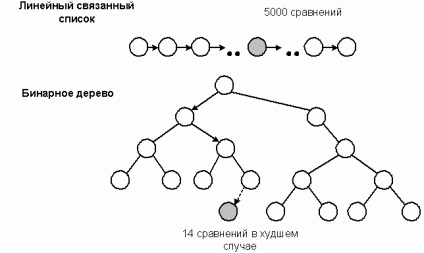
Tárolni az elemeket a fa ahhoz, hogy hatékonyan elérni, meg kell, hogy dolgozzon ki egy keresési struktúra, amely az útvonalat, hogy a tételt. Ez a szerkezet, az úgynevezett bináris kereső fába (bináris keresési fa) rendezi az elemeket az üzemeltető kapcsolatok "<". Чтобы сравнить узлы дерева, мы подразумеваем, что часть или все поле данных определено в качестве ключа и оператор "<" сравнивает ключи, когда добавляет элемент. Бинарное дерево поиска строится по следующему правилу:
Minden egyes csomópont, az adatok értéke a bal részfa ennél kevesebb csomópontot, majd a jobb oldali részfa - nagyobb vagy egyenlő.
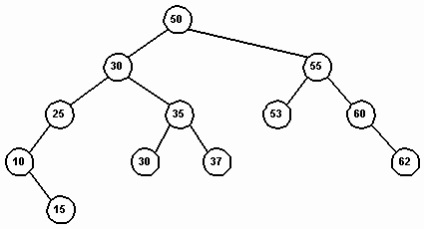
Ábra. 10. A bináris keresési fa
Ábra. A 10. ábra egy példát mutat a bináris keresési fa. Ez a fa az úgynevezett kereső, mert a keresést egy bizonyos eleme (kulcs), beszélhetünk csak nagyon speciális módon. Kezdve a gyökér, végignézzük a bal részfa, ha a kulcs-érték kevesebb, mint a jelenlegi csomópontot. Ellenkező esetben a beolvasott jobb részfa. Ez a módszer a fa lehetővé teszi a keresést elemet a legrövidebb utat a gyökér. Például egy keresést a 37. számú igényel négy összehasonlításban, a gyökértől kiindulva.
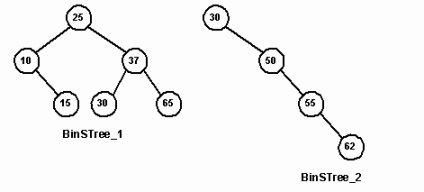
Ábra. 11. Példák a bináris keresés fák
Ábra. 11 csomópontok tartalmaznak csak egy egész értéket, hogy a kulcs. Ebben az esetben a csomópont 25 kulcsszerepet 25, és hasonlítsa össze a két csomópont összehasonlításával egészek. Az összehasonlítást a segítségével integrál operátorok kapcsolatok "<" и "==". Для студента университета ключом является ssn, и мы сравниваем две символьные строки. Это делается с помощью перегрузки операций. Например, следующий код реализует отношение "<" для двух объектов Student:
int üzemben <(const Student& s, const Student& t)
visszaút s.ssn A mi alkalmazás, adunk néhány példát kulcs / adat. Az illusztrációk, használjuk az egyszerű formában, ahol a kulcsot, és az adatok - ugyanaz a dolog. Munka bináris keresési fa Egy bináris keresési fa egy nem-lineáris szerkezete tárolására elemek sokaságát. Mint minden lista felépítése, a fa lehetővé kell tennie beszúrás, törlés, és keressen elemek. Kereséséhez fa szükséges ilyen betét műveletet helyesen van egy új elemet. Vegyük például, 8 csomópont betétet BinSTree_1 fa. Kezdve a gyökér 25 azt állapítja meg, hogy a 8 csomópontra kell lennie a bal részfa csomópont 25 (8<25). В узле 10 определяем, что место узла 8 должно быть в левом поддереве узла 10, которое в данный момент пусто. Узел 8 вставляется в дерево в качестве левого сына узла 10.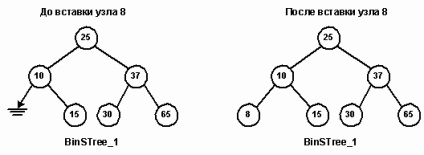
Mielőtt minden behelyezett Csomópontfa van egy meghatározott módon. Ugyanígy lehet használni, hogy keressen egy elemet. Keresés algoritmus a kulcsot, és keresi azt a bal vagy a jobb részfa minden tagja alkotó útját. Például, a keresési 30 elem a BinSTree_1 fán (ábra. 10.) kezdődik a gyökér csomópont 25, és bejut a jobb részfa (30> 25), majd a bal részfa. (30 <37). Поиск прекращается на третьем сравнении, когда ключ совпадает с числом 30, хранящемся в узле.
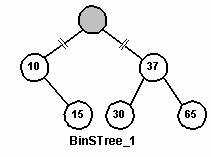
A láncolt lista csomópont eltávolítása műtét eltűnik, és összekapcsolja azt megelőző következő hop csomópontot. Egy bináris keresési fa, ez a művelet sokkal bonyolultabb, mert a csomópont árthatnak a megrendelő az elemek a fa. Tekintsük a feladatot eltávolítása a gyökér (amelynek értéke a kulcs 25) származó BinSTree_1. Ennek eredményeként, két elválasztott részfák, hogy az új gyökér szükséges.
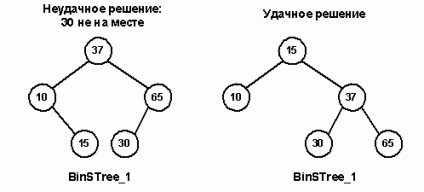
Első pillantásra azt sugallja, a döntés, hogy válasszon egy fia csomópont 25 - mondjuk, 37 - és helyette egy szülő. Azonban ez a megoldás nem egyszerű, mert annak egyes részei nem azon az oldalon a gyökér. Mivel ez a fa viszonylag kicsi, meg tudjuk állapítani, hogy a 15 vagy 30 elfogadható helyettesítője a gyökér.
// Class specifikáció BinSTree
sablon
cout <<"Студент отсутствует в базе данных." < Egy bináris keresési fa Class BinSTree - erős adatszerkezet, amely kezelésére használt dinamikus listákat. Mielőtt azonban egy példát a gyakorlati feladat az épület a megfelelési pillantást néhány egyszerű példát. Under Concordance alatt itt betűrendes listája minden szó egy adott szöveg a mutató a helyeken a látszat. Tekintsünk egy sor egyszerű programok, ahol a keresési fákat használnak. Létrehozása példák keresési fák. A szakasz „felépítése bináris fa» MakeCharTree funkció létrehozásához használt számos bináris fák karakteres adat. Hozzon hasonló MakeSearchTree funkció újonnan épített bináris keresési fák egész adatokat az Insert módszer. Először SearchTree_0 fa jön létre alapján arr0 tömb. Ebben a példában, a változó T típusú BinSTree. for (i = 0; i <6; i++) T.Insert (arr0 [i]); // hozzáadása elemet egy fa Újabb két fák, SearchTree_1 és SearchTree_2, hozzon létre magukat. Az első ilyen kell, hogy legyen a nyolc fa, és a második - a fa tíz véletlen számokat a tartományban 10-99 (12.). Száma termelt fa továbbítandó MakeSearchTree függvény paraméterként. Egy másik paraméter függvényében kell kapnia egy mutató a változó típusú BinSTree.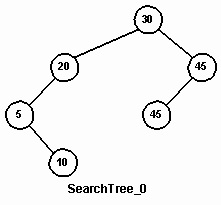
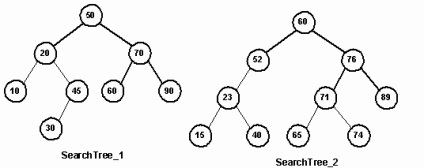
Ábra. 12. A fák által létrehozott függvények segítségével MakeSearchTree
Szimmetrikus átviteli módszer
A szimmetrikus tompított bináris fa látogatott először a bal részfa a csomópontot, majd - maga a csomópont, és végül a jobb részfa. Ha ezt a módszert alkalmazzák, hogy a folyosón egy bináris keresési fa, a csomópontok látogatott rendezett sorrendben. Ez a tény nyilvánvalóvá válik, ha összehasonlítjuk a csomópontok a részfa az aktuális csomópont. Minden alkatrész a bal részfa az aktuális csomópont kisebb értékeket, mint az aktuális csomópont, és minden csomópont a jobb részfa az aktuális csomópont nagyobb vagy egyenlő, mint az aktuális csomópont. Szimmetrikus tompított bináris fa biztosítja, hogy minden egyes csomóponthoz, amely meglátogatjuk az első alkalommal, kisebb egységek találhatók a bal részfa, és nagy - a jobb oldalon. Ennek eredményeként, a csomópontok áthaladni növekvő sorrendben.
Binary keresési fa lehet duplikált csomópontokat. Egy betét működését, továbbra is olvasni a jobb részfa ha új elemet egybeesik az adatokat az aktuális csomópont. Ennek eredményeként, a jobb részfa párosított rendelkező csomópont redundáns csomópontok.
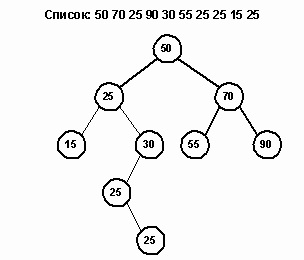
Például, a következő fa generált egy listát a 50 70 25 90 30 55 25 15 25.
Sok alkalmazás nem teszi lehetővé több csomóponttal, és használják a számláló adatmező esetben egy elem. Ez - az az elv összhang, ha a vonal számokat lánctalpas, amelyben a szó előfordul. Ahelyett, hogy egy párszor, hogy helyezze a szót, fa, dolgozzuk ismételt előfordulásait szó azáltal, hogy a sorszámok a listára.
Osztály megvalósítása BinSTree
osztály adatelemek BinSTree
Binary keresési fa határozza meg a gyökér pointer, amely a használt betét műveletek (Insert), keresés (Find) és a törlés (Delete). BinSTree gyökér osztály tartalmaz egy tételt egy mutató a gyökér, és amelynek kezdeti értéke NULL. Hozzáférés a gyökér GetRoot módszerrel hajtjuk végre, hogy a hívásokat külső funkciók folyosón. A második mutató, áram, meghatározza a fa helyét a frissítéseket. Keresse aktuális művelet van beállítva, hogy az egyező csomópont, és a mutatót a Frissítés funkció frissíteni az adatokat. Módszerek beillesztése és törlése az aktuális visszaáll egy új csomópont, vagy egy csomópont helyett a távoli. BinSTree objektum egy lista, amelynek mérete állandóan változik Insert és Delete funkciók. A jelenlegi elemek száma a listában tárolt privát tagja adatok mennyiségét.
// mutató a gyökér és a jelenlegi csomópont
// számos eleme a fa
Constructors, destruktor és értékadó operátor
sablon
BinSTree
// nem másolhatók a fa önmagában
ha (ez == jobb skála)
// Töröljük a jelenlegi fa.
// másolása új fa az aktuális objektumra