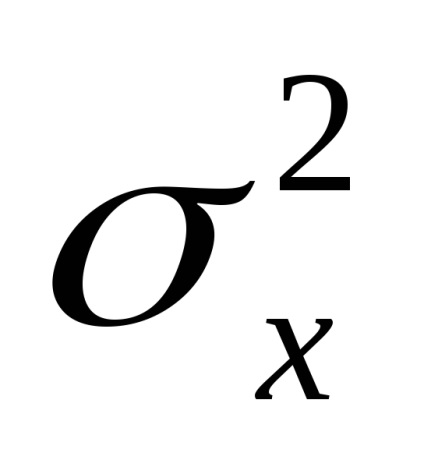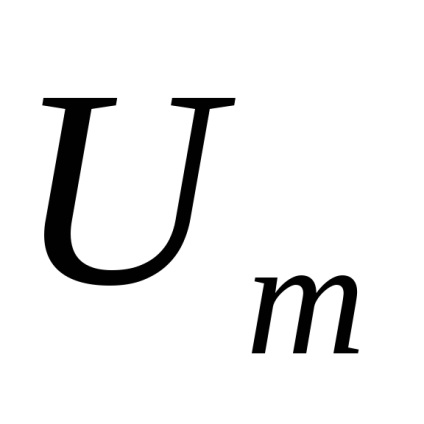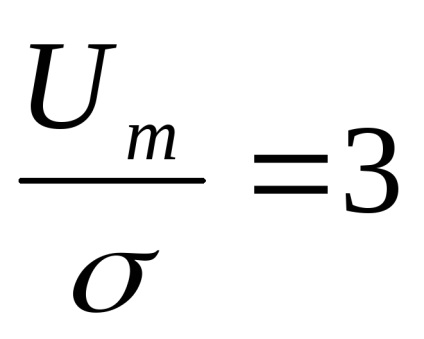15. Fehér zaj és tulajdonságai
stacionárius véletlenszerű folyamat állandó minden frekvencián a spektrális teljesítmény sűrűséget úgynevezett fehér zaj.
Szerint a Wiener-Khinchin funkciója fehér zaj korreláció:
nulla mindenhol, kivéve azon a ponton
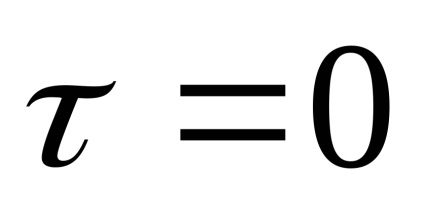
A fehér zaj egy delta-korrelációs folyamat. Korrelált pillanatnyi értéke a véletlenszerű jel végtelenül nagy változás mértéke az idő - nem számít, hogy milyen kicsi az intervallum volt

A fehér zaj egy absztrakt matematikai modell és a fizikai folyamat megfelelő, persze, nem létezik a természetben. Azonban ez nem zavarja helyett megközelítőleg valós elegendően széles sávú véletlenszerű fehér zaj folyamatok olyan esetekben, amikor a szalag átviteli áramkört, amely befolyásolja a véletlenszerű jel lényegében keskenyebb tényleges szélessége a zaj spektrum.
B) Gauss (normál) eloszlás.
Az elmélet a véletlen jelek alapvető fontosságú a Gauss valószínűségi sűrűség.
amely két numerikus paraméterrel m és
Cseréje változó
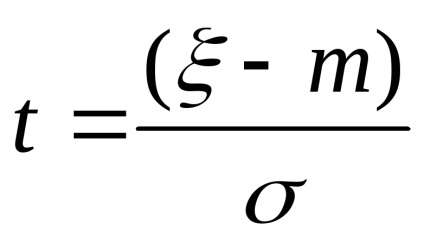
Van beépített valószínűség F
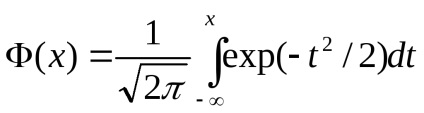
Ütemezés funkció F (x) formájában monoton görbe változó 0-1.
16..Uzkopolosny véletlenszerű folyamat. Rayleigh eloszlás. Törvény Rayleigh-Rice.
Megvizsgáljuk a tulajdonságait keskenysávú random jelet, amelynek spektrális teljesítménysűrűség van egy éles maximum közelében egy bizonyos frekvencia
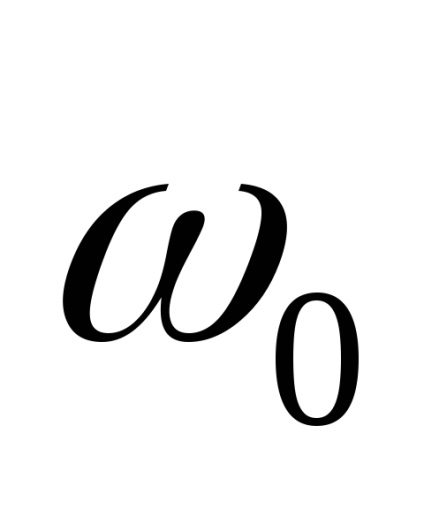
Tekintsünk egy stacionárius véletlenszerű folyamat x (t), egyoldalú teljesítmény spektrum, amely
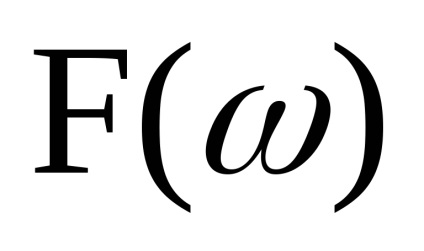
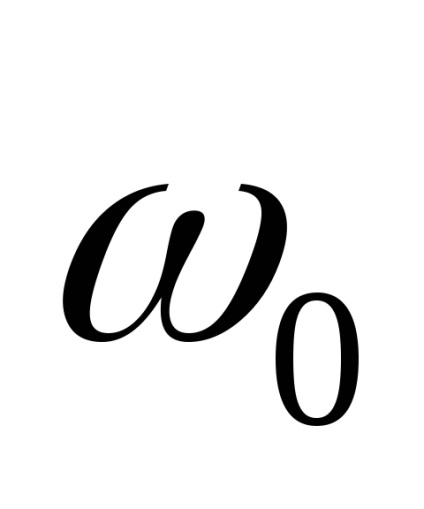
shift spektrumát a folyamatot a közelében a frekvencia
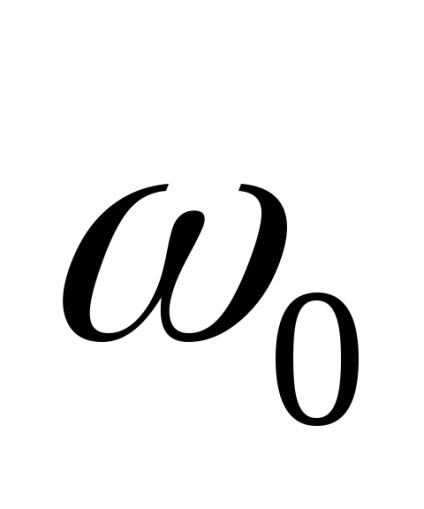
Átlagolása útján valószínűség-sűrűség (7,22), azt látjuk, az átlagos érték a borítékot, és a szórás:
Az egydimenziós valószínűségi sűrűség borítékot, meg lehet oldani számos problémát az elmélet keskeny véletlenszerű folyamatok, különösen annak a valószínűsége, a halad meg egy adott szintet a borítékot.
Véletlen változók által forgalmazott törvénye Rayleigh.
A legegyszerűbb feladat, hogy megtalálják a egydimenziós valószínűségi sűrűség a teljes boríték ingadozások. Tekintettel arra, hogy a hasznos jel, míg a zaj, írunk a kifejezés a teljes megvalósítás protsessaX (t). Ez a véletlenszerű folyamat uzkopolosen, ezért megvalósítása fejezhető ki a lassan változó ogibayuscheyU (T) és a kezdeti fázis
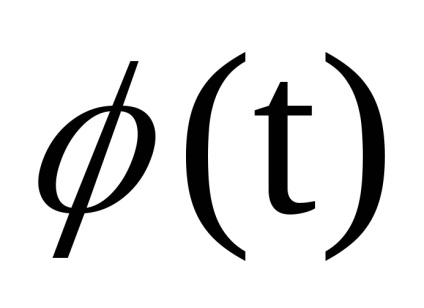
Az új változók van.
Most így egy egydimenziós valószínűségi sűrűség borítékon fel kell integrálni a jobb oldalon az (7.26) a szögkoordináta ahol találunk:
Ez az egyenlet fejezi ki a törvény, az úgynevezett Rice törvény. Megjegyezzük, hogy ha
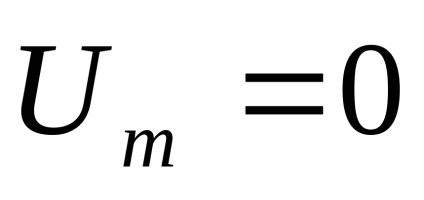
Behelyettesítve ezt a kifejezést (7,27), van
Ie borítékot a kapott jelet szét ebben az esetben közelítőleg normális a variancia