elméleti mechanika
Tekintsük a mérleg kar és alkotják a tervezet séma ható erők rajta (4. ábra). AB tartalék rúd tömeg -. G1 T E, és a rúd tömege CD -. G2 T F. A és C pontok helyébe rögzített hordozókat csuklósan reakciók Xa, Xc, Ya és Yc.
Ha figyelembe vesszük a konzol, mint egész, kiderül 4 ismeretlenek, és az egyensúlyi egyenletek tetszőleges sík rendszer erők teheti csak 3, így két tervezési rendszerek - minden egyes terminál számára külön-külön (5. ábra), míg a még 2 reakciók ismertek a D csuklón
Az egyes tervezési rendszer (5. ábra) van 3 egyensúlyi egyenlettel: kényszeríti a két egyenletet a nyúlványok a koordinátatengelyeken x és y, valamint az összeg a pillanatok erők adott m D ..


Az eredmény egy olyan rendszer 6 egyenletek hat ismeretlenek.
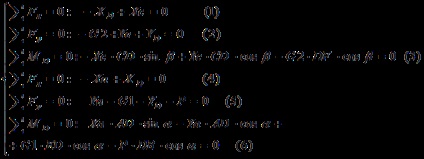
.
Behelyettesítve a (5) egyenletben és kiterjesztése:
Egyenletekből (1) és (4) találunk
.
Egyenletből (6) fejezzük Xa, (3) - Xc, és egyenlővé ezek a kifejezések:
Mi helyettesíti az Ya és átalakítja a kifejezést:
kifejezni, és megtalálja Yc:
Ahhoz, hogy megtalálja AD használja a tétel a szinusz:
Behelyettesítve számértékek kapjunk Yc = 160 (H); Ya = 150 (H); Xc = Xa = 135 (H)
Ellenőrizze. A teszt a legjobb felhasználása az összes konzol tervezet séma (4. ábra) - Ez a számítás rendszer nem a csukló magában foglalja a reakciók D. alkotnak az egyensúlyi egyenlettel formájában az összeg a nyomatékok bármely pont (például, viszonyítva D pont) (4. ábra), és ellenőrzi hogy ez lesz az identitás:
Valóban, ebben az esetben a kapott értékeket kapunk egy identitását.
A reakciót Yc = 160 (H); Ya = 150 (H); Xc = Xa = 135 (H).
Számítógépes Számítások:
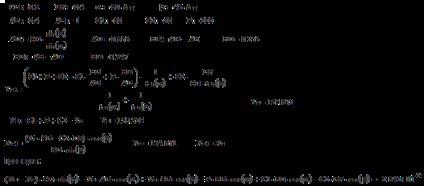
Mi megoldjuk etuzhe feladat Mathcad iteratív módszer:

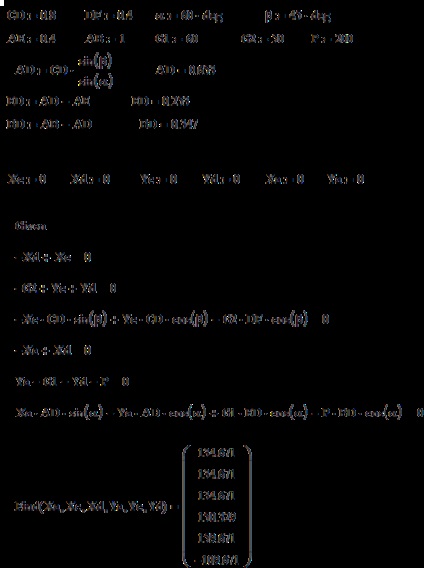
Példa SP-5. Egyensúlyi térbeli rendszer erők (Meshchersky, 8,24)
Homogén tömeg négyszögletes keret 200 csatlakozik a falhoz H útján gömbcsukló A és hurok B, és tartott vízszintes helyzetben CE kötelet kötött a keret és a C pont E köröm hajtott a falba függőlegesen ugyanabban a vonal, és a
. Határozza meg a feszültség a kötelet, és a csapágy reakciók.
Amikor az előre meghatározott numerikus értéket kapunk a T = 200 H, XA = 86,6 H, YA = 150 H, ZA = 100 H, XB = ZB = 0.
Ellenőrizze. Ellenőrzésére a három egyensúlyi egyenletek formájában előrejelzések erőket a x1 tengely. y, z1 (6. ábra), és ellenőrzi, hogy ez lesz az identitás:
Sőt, azt kapjuk, helyettesítve a mért értékeket
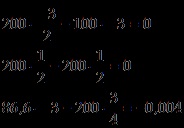
Válasz. A húzóerő T = 200 N, a támogató reakció XA = 86,6 H, YA = 150 N, ZA = 100 N, XB = YB = 0.
Számítógépes megoldás. Hogy oldja meg a lineáris egyenletrendszer lehet használni, például egy mátrix módszer. Az egyensúlyi egyenletek (1), (2) és (3) írt egy szabványos formátumban, miközben ismeretlenek a bal oldalán egyenletek:
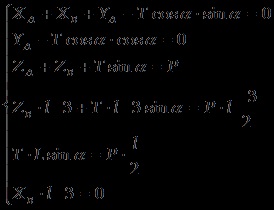
Matrix megoldás formájában:
