Plakálás a mathcadban
Műalkotás címe: Grafika a Mathcad-ban
Terület: Informatika, Cybernetics és Programozás
Leírás: Ehhez ismerni kell az érintő és a normál grafikonok egyenleteit. Nem ismerem őket, ezért fordítottam a hatalmas internetre. Ebben találtam meg a webhelyet, igen, tárolja a hatalmas Mozilla Firefox böngészőjét, amely megmutatta nekem a hülye szolgát, a szükséges funkciók egyenletét.
Fájlméret: 181.5 KB
A munkát letöltötték: 38 fő.
Az Orosz Föderáció Oktatási és Tudományügyi Minisztériuma
RYBINSKY STATE AVIATION TECHNIKAI EGYETEM nevű. P.A Solovyev
Rádiótudományi, Elektronikai és Informatikai Kar
informatika
A SPD-13 Pestov VV csoport hallgatója
Kód Aláírás, dátum
Tanár Pinaev V.N.
Egy adott funkcióhoz.
1. Mutassuk be az első és a második származék függvényét és grafikonjait a koordinátákban.
2. Az érintő és a normál görbéket a (x 0 = 3) 0 pontban a függvényhez hozzák létre.
3. Keresse meg az f (x) függvény helyi extremum pontját és az inflexiós pontokat (állópontok).
4. Határozza meg a funkció értékét álló helyzetekben.
5. Határozzuk meg a primitív + c-t és hozzuk létre a primitív család grafikonjait.
1. Mutassuk be az első és a második származék függvényét és grafikonjait a koordinátákban.
Egy függvény és két származékainak grafikonjának Mathcad-ba történő előállításához meg kell szerezni a származékok első és második származékát. Megteheti magad, programok használata nélkül:
e - x + x * (e - x) '= e - x - x * e - x = e - x * (1- x)
Most, hogy kiszámolom mindkét származékot, itt az ideje, hogy grafikaikat Mathcad-ba építsék. Ez rám derült ki, hogy az 1. ábrán látható:
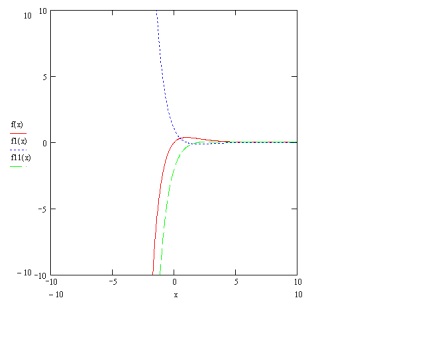
A piros vonal a funkció grafikonját mutatja, zöld és kék - az első és a második származék grafikonjait.
Tehát az első feladat megtörtént.
2. Szükséges a tangens és a normál grafikonok ábrázolása a függvénygrafikonhoz.
Az érintő egyenlete a következő:
y = f '(x0) * x + f (x0) -f' (x0) * x 0
A normál egyenletnek a következő alakja van:
y = f (x0) - (x-x0) / f '(x 0)
Ahol x 0 = 3 (a feltétel által megadott pont).
Most, hogy van egyenletem, még meg kell írni őket a Mathcad programban. Itt találhatók a grafikonok (2. ábra):
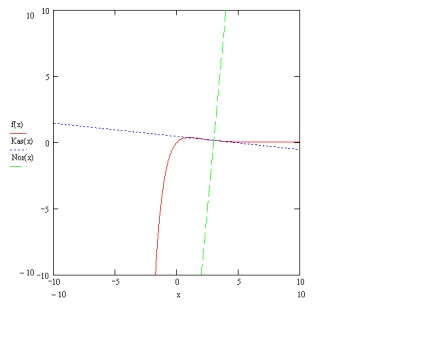
A piros vonal a függvénygrafikon, a kék a x-es ponton a grafikon érintője. A zöld az x 0 ponton a grafikonra normális.
A 2. feladat teljesítettnek tekinthető.
3. Keresse meg az f (x) függvény helyi extremum pontját és az inflexiós pontokat (állópontok).
A helyi extremum pontok megtalálásához a függvény első származékát nullára kell sorolni.
f '(x) = 0; e - x * (1 - x) = 0; 1- x = 0;
x = 1 kritikus pont, ugyancsak helyhez kötött (a kritikus pont az a pont, ahol a függvény megváltoztatja az "irányát": ha növekszik, akkor csökken (az én esetemben) és fordítva). Állandó pont olyan pont, ahol a származék nulla.
Ezzel a feladattal foglalkoztam is.
4. Határozza meg a funkció értékét álló helyzetekben.
Nos, elég egyszerű. Elég az x = 1 pont helyettesítése a függvény egyenletében:
Úgy döntöttem, hogy numerikus formában mutatom be az értéket, egyenlő lesz:
Tehát ez a feladat megtörtént, az utolsó marad.
5. Határozzuk meg a primitív + c-t és hozzuk létre a primitív család grafikonjait.
Engedtem magamnak, hogy ne változtassam meg a nyelvet, mert nem akartam megsérteni a webhely bájos formáját. És most már megvan az antiderivatív egyenlet. De egy primitív családot kell létrehoznom. Már kezdtem aggódni, mert csak egy képletem van, és néhány diagramot fel kell készíteni, amíg nem kérik, hogy változtassak állandóan. És most írok képleteket Mathcad-ban, és egy csoda után a primitív család grafikái készen állnak nekem (3.
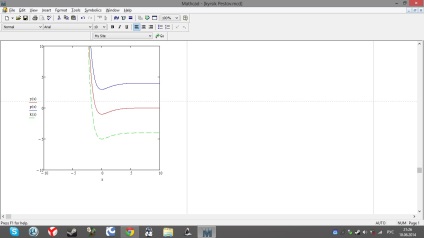
A piros vonal jelzi a prototípust, ahol const = 0, és a másik const = 4; -4.
Tehát az én kurzusomat elvégeztem. Ideje összefoglalni.
E munka során olyan csodálatos programot tanultam, mint Mathcad. Vettem egy kis készség a kezelése során, és ismét meggyőzte e megváltoztathatatlan fenséges ember teremtése, mint az internet, mert előtte, mi esik térdre, ez a mi gyerek, ami szinte rabszolgává minket. És én, megvetõ szolgám, hajoljam elõtte. És én köszönöm a mentorok, Pinaeva Vlagyimir Nyikolajevics és Shalaev Dmitrij Szergejevics, ami miatt az ilyen szolga, ahogy tanulta, és képes volt elsajátítani a program Mathcad.