5 Építsen háromdimenziós grafikonokat a scilab-ban
2. A z ij = f (x i; y j) függvény értékeinek kiszámítása minden rács csomóponton.
3. Felhívás a háromdimenziós grafikonok létrehozására.
5.1 Funkciók plot3d és plot3d1
A Scilab-ban a felület a plot3d vagy a plot3d1 függvényekkel konstruálható. A különbség az, hogy a plot3d egy felszínt és egy öböl-
annak egy színét, és plot3d1 a felszínt, amelynek minden egyes cellája színt ad, függően a függvény értékétől a rács mindegyik csomópontjában (lásd az 5.11. ábrát).
A funkciók hívása a következő:
5.1. A plot3d és plot3d1 függvények
itt x az abszcissza értékek oszlop vektora;
y ordináták értékeinek vektor-oszlopa;
z a függvény értékeinek mátrixa;
theta, alpha valós számok, amelyek a grafikonon a látószög gömb alakú koordinátáit fokban határozzák meg. Egyszerűen fogalmazva, ez a szög, ahol a megfigyelő látja a megjelenített felületet;
láb jelezze a grafikon szimbólumok koordinátatengelyeit a @ jel által elválasztott. Például: "X @ Y @ Z".
három összetett paraméterből álló zászló tömb: [mód, típus, doboz]. itt
mód határozza meg a felület színét (lásd 5.1 táblázat). Az alapértelmezés szerint 2 töltés színkék, a négyszögletes rács jelenik meg.
5.1 táblázat. Az üzemmód paraméter értékei
> 0 a felület ¾mode¿ színű, egy négyszögletes rács van rajzolva
0 egy téglalap alakú rácsot jelenít meg, nincs kitöltés (fehér szín)
<0 поверхность имеет цвет ¾mode¿, отсутствует прямоугольная сетка
típus lehetővé teszi a grafikon méretének szabályozását (lásd az 5.2. táblázatot), alapértelmezés szerint 2-es értékkel rendelkezik;
(lásd 5.3 táblázat). Az alapértelmezett érték 4.
Az ebox meghatározza annak a területnek a határait, amelyre a felület kimenet lesz, mint vektor [xmin, xmax, ymin, ymax, zmin, zmax]. Ezt a paramétert csak a type parameter = 1 értékére lehet használni.
keyn = a grafikon tulajdonságainak értékeinek sorrendje1 = érték1, kulcs2 = érték2. keyn = valuen,
mint pl. a vonal vastagsága, színe, a grafikus ablak hátterének kitöltési színe, marker jelenléte stb. (lásd a 4.6.
Tehát a plot3d (plot3d1) függvényeket paraméterként kell átvinni egy négyszögletes rácsra és egy érték mátrixra a rács csomópontjaiban.
Konstruáljon egy függvény Z = sin (t) cos (t) függvényét.
Hozzon létre egy értéktartományt a t argumentumhoz. Kiszámítjuk a függvény értékeit és írjuk őket a Z tömbbe.
Vegyük észre, hogy amikor a plot3d függvényt X és Y paraméterként érjük el, négyszögletes rácsot adunk meg, a t paraméter kétszer van megadva, mivel mind a sin és cos függvény egy t változótól függ (lásd az 5.1.
Lista 5.1. A Z = sin (t) cos (t) függvény plotja a plot3d segítségével
Most bonyolítsuk meg a feladatot. Olyan felületet hozunk létre, amelynek egyenletét két független változó adja.
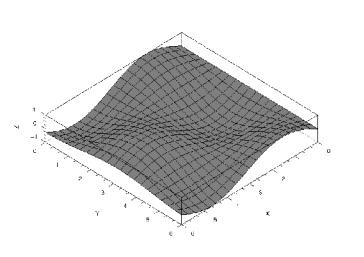
Legyen egy függvény grafikonja Z = 5y 2 x 2.
5.1. A plot3d és plot3d1 függvények
Ábra. 5.1. A függvény grafikonja Z = sin (t) cos (t)
Először is meg kell adnunk az X és Y tömböket.
Ezután létrehozzuk a Z (x i; y j) függvény értékeinek mátrixát, a hurok for utasításával. Itt i a hurokparaméter, amely átmegy az X tömb minden értékén, és j a hurokparaméter, amely az X tömb minden egyes értékét leképezi az Y tömb minden értékére.
Így a Z függvénynek minden változó értéke Y-val (az elsőtől a tömb utolsó értékéig) és az X tömb első értékének kiszámításával először, majd az X tömb második értékével stb.
Visszahívás, hossz határozza meg az X (Y) tömb elemeinek számát (lásd 2. fejezet).
Végül a felszín felépítéséhez a3d1 függvényhez fordulunk (ld
Ábra, 5.12 ábra).
Amint azt a példaből láthatjuk, csak a plot3d függvény segítségével grafikusan megjeleníthet két független változótól függő mutatót. A Scilab-ban több parancs van, amelyek megkönnyítik a négyszögletes rács létrehozását: a genfac3d és az eval3dp.
A legegyszerűbb a szintaxis alapján a genfac3d függvény:
Itt xx, yy, zz a (4, n 1 m 1) méretű eredményt adó mátrix, ahol xx (:, i), yy (:, i) és zz (i, i) a négyszögletes rács egyes celláinak koordinátái;
x m méretű x koordináták vektora;
y y-koordinátájú y vektor az n méretben;
z a Z (x i; y j) függvény értékeinek mértéke (m; n) mátrixa.
Konstruáljon egy függvény Z = sin (t) cos (t) függvényét.
Határozzuk meg a t paraméter tömbjét, és számítsuk ki a Z = sin (t) cos (t) függvény értékeit. Téglalap alakú rácsot hozunk létre a genfac3d paranccsal (lásd a 5.3.
Lista 5.3. Hozz létre egy négyszögletes rácsot a genfac3d paranccsal, és ábrázolja a grafikont a plot3d függvény használatával
A grafikon elkészítéséhez kapcsoljuk be a plot3d függvényt (lásd az 5.1. Ábrát). A genfac3d parancs hátránya, hogy mégsem egyszerűsíti
a függvény plot3d-vel való munkát, ha a felületet két változó függvénye adja. Ebben az esetben az eval3dp parancsot kell használni:
Xf, Yf, Zf a méret (4; n 1 m 1) eredményező mátrixa, ahol xx (:, i), yy (:, i) és zz (i, i) a négyszögletes rács egyes celláinak koordinátái;
szórakoztató egy olyan funkció, amelyet a felhasználó definiál egy háromdimenziós grafikonra;
5.1. A plot3d és plot3d1 függvények
m méretű p1 vektor;
p2 az n méretű vektor.
Mutassuk be az eval3dp parancs hatását a következő példával.
A következő egyenletekből adható grafikonot: x = p 1 sin (p 1) cos (p 2), y = p 1 cos (p 1) cos (p 2), z = p 1 sin (p2).
Először is meghatároztuk a p 1 és p paraméterek értékeinek tömböket. Ezután hoztuk létre a scp függvényt, amely a grafikont állítja be.
Emlékezzünk arra, hogy a Scilab funkciók a deff parancs használatával készülnek:
ahol s1, s2. a kimeneti paraméterek listája, azaz azok a változók, amelyekre a számítások végeredményét hozzárendelik;
új funkció a létrehozandó függvény neve;
e1, e2. bemeneti paraméterek.
Ne felejtsük el, hogy a deff parancsot csak három sorban írjuk, hogy megkönnyítsük a listát (lásd 5.4).
Lista 5.4. Hozzon létre egy téglalap alakú rácsot az eval3dp használatával, és ábrázolja a grafikont a plot3d segítségével
p2 = linspace (0,2 *% pi, 10); (p1). * cos (p2) ";" y = p1. * cos (p1). * cos (p2) ";
"z = p1. * sin (p2)"]); [Xf, Yf, Zf] = eval3dp (scp, p1, p2); plot3d (Xf, Yf, Zf);
Most hozzon létre egy téglalap alakú hálózatot az eval3dp parancs segítségével, és rajzolja be a diagramot a plot3d függvény használatával (lásd az 5.13. Ábrát).