Prism - egy előadás geometria

1) meghatározása a prizma. 2) típusú prizmák: - prizma; - ferde hasáb; - a jobb hasáb; 3.) A teljes felülete a prizma. 4.) A terület a palástfelület a prizma. 5.) Volume prizma. 6) Mi bizonyítja tétel egy háromszög alakú prizma. 7.) bizonyítják tétel tetszőleges prizma. 8.) A keresztmetszetek a prizmák: - egy merőleges keresztmetszete a prizma; 9.) A prizmák találkozott az életben.

Meghatározása prizmák: A1A2 ... AnV1V2Vn- prizma sokszögek A1A2 ... A n és V1V2 ... Bn - prizma bázis A1A2V2V1 paralelogrammák, A1A2V2V1 ... AnA1V1Vn - oldalfelületei szegmensek A1B1, A2B2 ... AnBn - oldalirányú bordák Prism prizma nevezzük poliéder, amelynek két arca (bázisok) fekszenek egymással párhuzamos síkokban, és minden élek kívül ezeknek a felületeknek párhuzamosak egymással. Prism arc eltérő okból, az úgynevezett oldalfelületek. és a szélük nevezzük oldalsó élei. Minden oldalsó szélei egyenlő, mint párhuzamos szegmensek, által határolt két párhuzamos síkban. Minden oldalán arcok a hasáb paralelogramma. Alkalmas bázisok a prizma egyenlő és párhuzamos oldalú. Ezért az alapon, egyenlő sokszög. A felület a prizma két bázisok és oldalsó felületek. A magasság a prizma nevezzük szegmenshez közös merőleges síktól, amelyben fekszenek a prizma bázis. A magasság a prizmák megegyezik a h távolság a síkok közötti a bázisok.
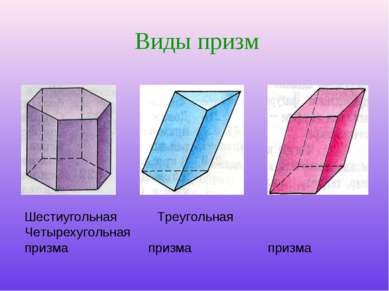
Típusai hatszögletű hasáb háromszögű prizma négyszögletű prizma prizma