Funkcionális sorozat (a koncepció működőképes sorozat
Hasonlóképpen, megszorozzuk az egyenlet (3,49), és az integráló előtti, kapjuk:
,
Így, az együtthatók számát és (3,49) egyedileg meghatározott (3.50) - (3,52), ami azt bizonyítja, az alábbi tétel.
Ez a tétel ad okot, hogy vezessenek be a következő meghatározást.
Definíció. Funkcionális sorozat formájában:
ha az együtthatók által meghatározott képletek:
nevezett közelében Furefunktsiif (x). Figyeljük meg, hogy mindig.
Engedje meg, hogy milyen tulajdonságokkal kell rendelkeznie az f (x), a Fourier-sor épített rá, hogy közelednek, és hogy az összeg a Fourier sor épített azonos értékeket ennek a funkciónak a megfelelő pontokat.
Definíció. A f (x) nevezzük szakaszonként monoton szegmens [a. b], ha a szegmens lehet törni egy véges számú pontot időközönként úgy, hogy mindegyikük a függvény monoton.
A definíció következik, hogy ha az f (x) - szakaszonként monoton és határolt intervallumba [a. b], akkor csak egy elsőrendű töréspontot. Valóban, ha van egy olyan pont a diszkontinuitás az f (x), akkor ott vannak határok miatt a monotónia funkció:
azaz pont az első fajta a lényeg a diszkontinuitás (ábra. 3.4).
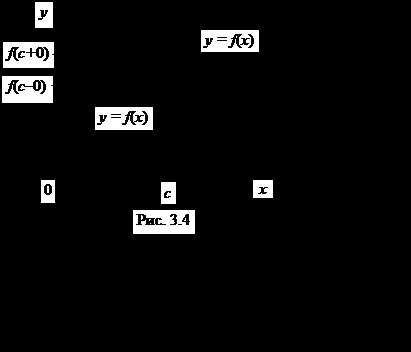
Tétel 3.7. Ha az f (x) periodikus egy időszak, amely egy szakaszonként monoton és határolja az intervallumban, majd a
minden folytonossági pontjában (vagyis az összege a Fourier-sor). Ha a pont - a pont diszkontinuitás az első fajta funkció, az összeget a Fourier sor ezen a ponton
,
ahol - túl a bal, illetve jobb oldalon, azon a ponton, x.
Ebből következik, hogy a tétel a folytonosság a funkció pont, és az összeg megegyezik a számtani átlaga a bal és jobb határok funkciót pontok diszkontinuitás az első ilyen.
A tétel azt is, hogy az osztály a funkciót lehet képviselő Fourier, meglehetősen széles. Ezért Fourier széles körben használják a matematika különböző ágaiban. Különösen sikeres Fourier használják a matematikai fizika és annak alkalmazása konkrét problémák a mechanika és a fizika.
1. példa bomlanak funkciónak egy Fourier-sor, amelynek olyan időtartamon át és egy előre meghatározott intervallumban a következőképpen: