№5-mechanika előadás
1.Normalnye húzófeszültség és nyomó
2. meghatározása a hosszirányú és keresztirányú törzs. Hooke-törvény
3. statikailag határozatlan probléma
4. termikus feszültségek
5. Feszített
1. Normál hangsúlyozza feszültség és a tömörítés
Ha a felület a prizmatikus rúd rácsvonalakat alkalmazott párhuzamos és arra merőleges a rúd tengelyével, és hogy gyakoroljon húzóerőt hozzá, lehetséges annak biztosítása, hogy a rácsvonalak és a deformáció után maradnak egymásra merőleges (lásd. Ábra. 1).
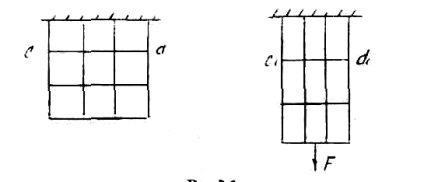
Minden vízszintes vonalak, például CD lefelé mozog, miközben megmaradt a vízszintes és egyenes. Azt is feltételezik, hogy a belsejében a rúd ugyanazt a mintát, azaz A „keresztirányú keresztmetszete a rúd, lapos és a normális, hogy a tengelye alakváltozás előtt is lapos és tengelyére merőleges deformáció után.” Ez a fontos hipotézis ismert hipotézisét sík szakaszok vagy Bernoulli hipotézist. A képletek kapott alapján ezt a hipotézist, által támogatott kísérletek eredményeit.
Ez a minta deformációja ad okot azt hinni, hogy a keresztmetszet csak a névleges feszültség, ugyanaz minden pontban a szakasz, és a nyírási feszültségek nulla. Ha fellépő nyíró igénybevételnek lenne megfigyelhető szögletes alakváltozás, és a szögek között a hosszirányú és keresztirányú vonalak veszti egyenes. Ha a normál feszültségek nem voltak azonosak minden részén pontok, ahol a feszültség nagyobb lenne és alakváltozás, és ezért a keresztmetszet nem lenne lapos és párhuzamos. Miután elfogadták azt a hipotézist, a sík szakaszok megállapítjuk, hogy.
Mivel a hosszirányú erő az eredő a belső erők
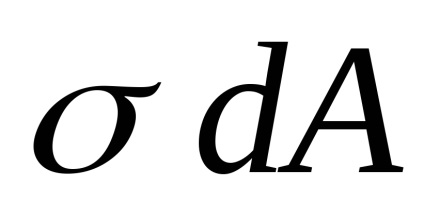
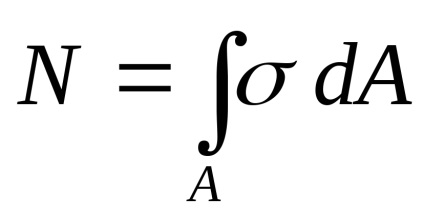
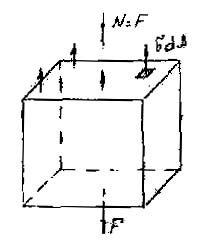
Az állandók kivinni az integrál jel:
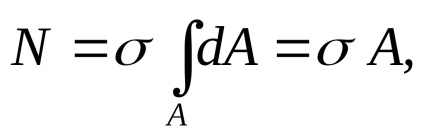
ahol A keresztmetszeti területe.
A formula találni a normális húzófeszültség vagy kompressziós:
Ez az egyik legfontosabb képletek a szilárdságtani így fog kiosztani a kereteket, és az is csinálni a jövőben.
nyújtható

Amikor a fa az egyetlen érvényes külső erő F.
és a feszültség lehet meghatározni a következő képlettel:
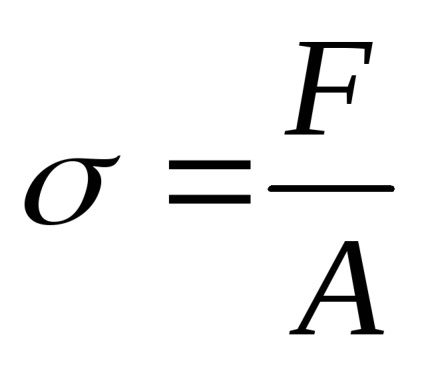
2. meghatározása a hosszanti és keresztirányú törzs
Az elasztikus szakaszában a legtöbb építőanyag stressz és a törzs kapcsolatos közvetlen befolyása az úgynevezett Hooke-törvény:
ahol E modulusa hosszanti rugalmassági vagy Young modulus, mért MPa, jellemzi az anyag merevsége, azaz képes ellenállni deformáció, a megadott érték esetén tablitsax könyvtárban;


l eredeti hosszát, m.
Minél magasabb az érték a hosszanti E rugalmassági modulus, a kevésbé deformáció. Például, az acél E = 2,110 5 MPa, és az öntöttvas E = (0,75 ... 1,6) 10 5 MPa, így a tervezés a vas elem veszi nagy alakváltozás azonos körülmények között eltérő acél. Nem szabad összekeverni azzal a ténnyel, hogy a hajtott megtörni a rúd acél lesz egy sokkal nagyobb törzs, mint a vas. Ez nem a korlátozó deformáció és a rugalmas alakváltozás fázisban, azaz bekövetkezése nélkül képlékeny, és ugyanazt a terhelést.
Transform Hooke-törvény helyett az egyenlet (3.3):
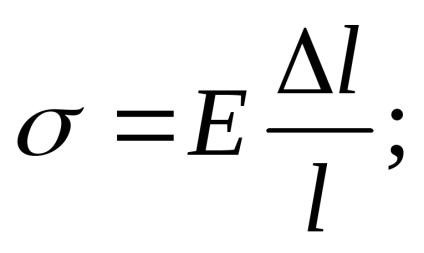
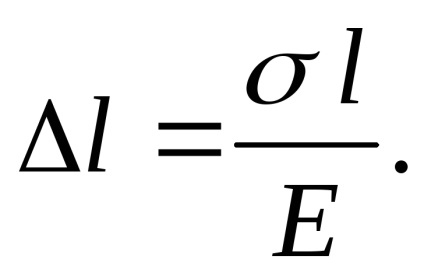
helyettesítheti az értéket

Kaptunk egy képletet abszolút nyúlás (rövidülés) a rúd. nyújtható

Szakító rúd elvékonyodik, amikor a sűrített oszlopon. Megváltoztatása keresztmetszeti méretei az úgynevezett keresztirányú törzs. Például, egy négyszögletes keresztmetszetű betöltés előtt voltak a b szélessége és magassága szakasz h. és berakodás után b1 és h1. Relatív keresztirányú alakváltozás a keresztmetszet szélesség:
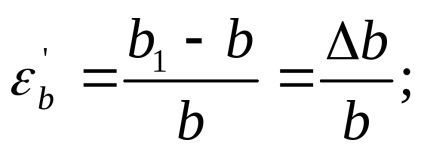
keresztmetszet magassága:
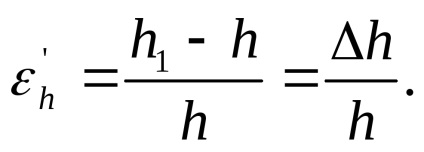
Izotrop anyagok tulajdonságai ugyanazok minden irányban. ezért:
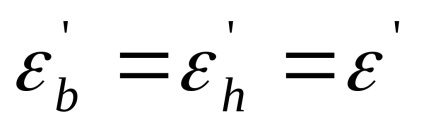
Húzó-nyíró alakváltozás negatív nyomó pozitív.
Az arány a keresztirányú törzs a hosszanti törzset nevezzük a keresztirányú Poisson-tényezője és együttható:
Megállapítást nyert, kísérletileg, hogy a rugalmas anyag bármely szakaszában a munka értéke
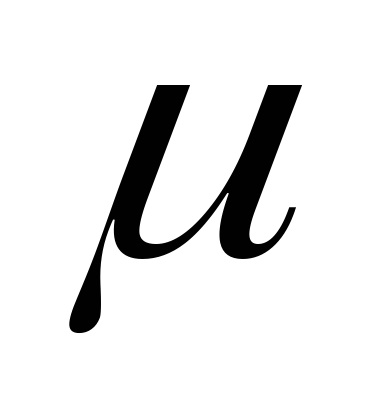
lehet beszerezni a függőség a következő általános képletű (5):
Szakítószilárdság (nyomó) keresztirányú gerendák mozog hosszanti irányban. Mozgó egy deformációja következtében, de a két fogalom világosan meg kell különböztetni. Egy rúd (lásd. Ábra. 3), hogy meghatározzuk az alakváltozás nagysága és elmozdulás Epure konstrukciót.
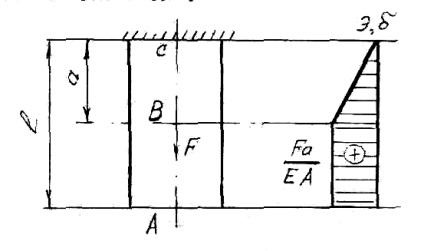
Amint az ábrából látható AB rudat szegmens nem feszített, de lesz elmozdulás miatt meghosszabbított szegmens CB. A nyúlás:
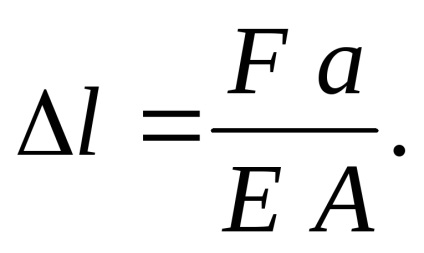
Mozgassa a keresztmetszetek jelöljük



3. statikailag határozatlan probléma
Statikailag határozatlan rendszer tekinthető, erőfeszítéseket, amelyeket nem lehet meghatározni a segítségével egyetlen egyenletek statika. Minden statikailag határozatlan rendszerek „extra” linkek formájában kiegészítő rögzítési pontok, csapok és más elemeket. „Extra” az ilyen kapcsolatok nevezzük, mert ezek nem szükségesek szempontjából egyensúlyi vagy annak geometriai állandóság, és az egység folytat strukturális vagy működési célokat.
A különbség az ismeretlenek száma, és a több független egyensúlyi egyenletek, hogy lehet a rendszer, jellemzi száma redundáns ismeretlenek vagy foka redundancia.
Statikailag határozatlan egyenletrendszer megoldható összeállítása mozgása bizonyos pontjainak a száma, melynek meg kell egyeznie, hogy milyen mértékű határozatlanság rendszer.
Legyen egy rúd szorosan lezárt mindkét végén, az F erő (lásd. Ábra. 4). Mi határozza meg a támogatás reakciókat.
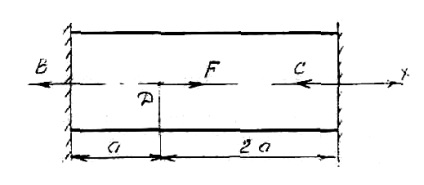
Reakció támogatja a közvetlen a bal oldalon, mert az F erő hat, hogy a jobb oldalon. Mivel a súlyerő aktus csak egy egyenlet statikus egyensúly alakítható ki egy sort:
Tehát, két ismeretlen reakciók támaszok B és C egy egyenlet statikus egyensúly. A rendszer egyszerre statikailag határozatlan. Ezért, hogy oldja meg kell tenni egy további egyenlet alapján az elmozdulás a C ponton Értelmi dobja ki a megfelelő támogatást. A bal oldali része az erők F VD szár kinyúlik és a keresztmetszete C jobbra tolódik el a mennyisége ezt a deformáció:
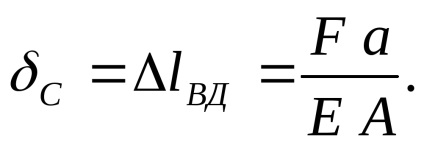
A padlótól reakciót C lesz tömörítve, és a rúd részben balra mozog, a mennyiségét deformáció a teljes rudat:
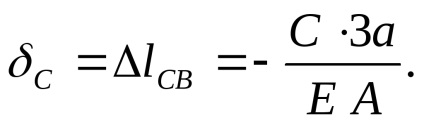
A támogatás nem teszi lehetővé a szakaszt egy lépés, hogy a bal vagy a jobb, így a mozgás mértékét az F erő és C legyen egyenlő nullával:
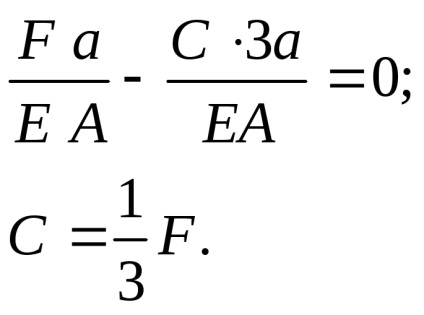
Behelyettesítve a értéke C az egyenletben a statikus egyensúly, határozza meg a második emeleten reakció:
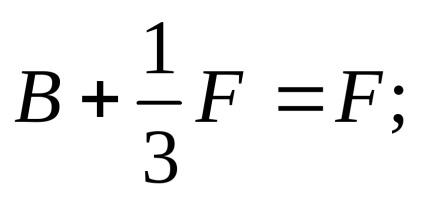
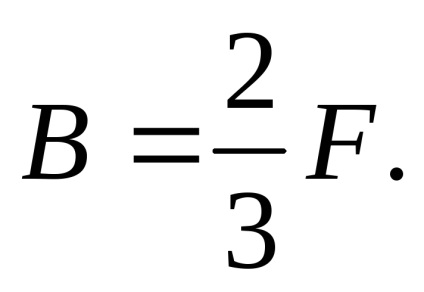
4. termikus feszültségek
A statikailag határozatlan rendszerekben a hőmérséklet változására előfordulhatnak feszültség. Hagyja a rúd szorosan lezárt mindkét végén van hőmérsékletre melegítjük

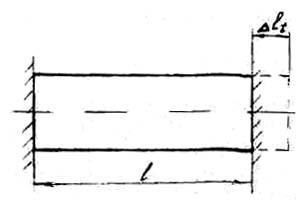
Amikor a test melegítjük, expandált, és a rúd hajlamosak hosszúkás értéke:
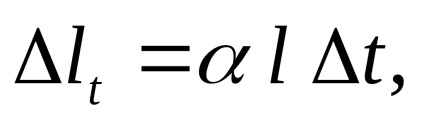
ahol

l eredeti hosszát.
Support nem teszik lehetővé a rúd, hogy meghosszabbítsák, így a rúd összenyomja mennyiségben:
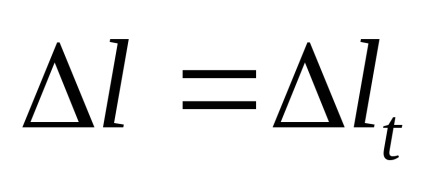
Általános képlet szerint (4):
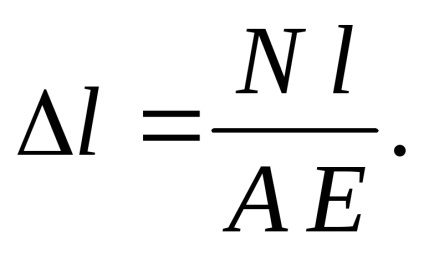
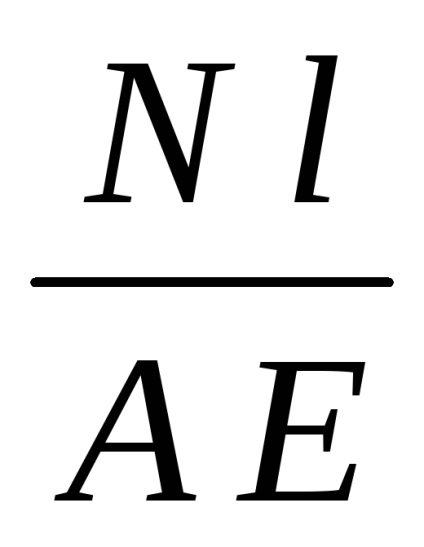
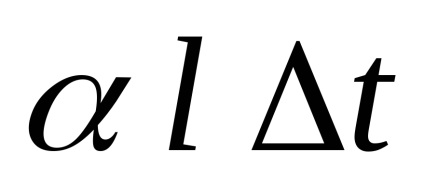
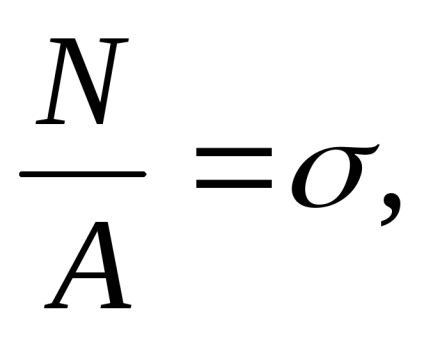
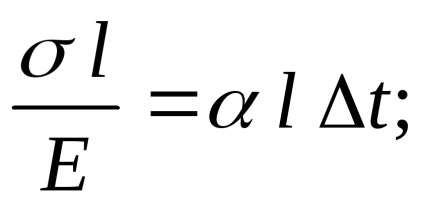
Amint látható, a (7) képletű termikus feszültségek függetlenek a hossza a rúd, és csak attól függ a lineáris hőtágulási együttható, modulusa hosszanti rugalmasságát és hőmérséklet-változások.
Termikus feszültségek magas értékeket érhet el. Hogy csökkentsék a kialakítás egy speciális hőmérsékleten rések (például réseket az ízületekben a sínek), vagy a kompenzációs eszköz (például, könyökök a csövek).
5. Feszített
építési elemek lehetnek eltérést méretű gyártás során (például miatt hegesztés). Összeállításakor a méretek nem egyeznek (például furatok), és annak érdekében, hogy össze alkatrészeket. Ennek eredményeként, vannak olyan belső erők alkalmazása nélkül, a külső terhelések szerkezeti elemek.
Legyen két merev végződések behelyezett rúd, amelynek hossza nagyobb, mint a távolság értéke közötti A támaszok (lásd. Ábra. 6.). A tengely fogja tapasztalni tömörítés. Meghatározzuk a feszültség, a következő képlet segítségével (4):
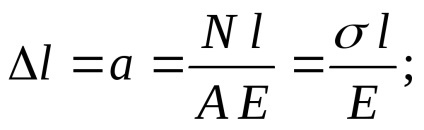

Amint látható, a (8) képletű szerelési hiba feszültség egyenesen arányos, és a mérete. Ezért kívánatos, hogy a = 0. különösen egy kis hosszúságú rudak volna

Azonban egy statikailag határozatlan rendszerek szerelési feszültségek specifikusan igénybe, hogy növeljék a csapágy kapacitását a szerkezet.