Tudd Intuíció, előadás típusú matematikai modellek
2.2. Szimulációs rendszer folyamatos Markov folyamat
Van egy széles osztálya rendszerek, amelyek megváltoztatják az állapotát véletlenszerű időpontokban. Csakúgy, mint az előző esetben, ezekben a rendszerekben foglalkozik a folyamat diszkrét állapotok. Például, mozgó az objektumot a üzemképes a hibás aránya erők a csatában, és így tovább. N. hatékonyságának értékelése az ilyen rendszerek alkalmazásával is meghatározható a valószínűségek minden állapot bármikor.
Annak megállapításához, a valószínűsége, hogy a rendszer állapotát bármely szakában használatához szükséges matematikai modellt Markov folyamatok folyamatos idő (folyamatos Markov folyamatok).
A szimuláció során a rendszerek folyamatos Markov-folyamatok nem tudjuk kihasználni az átmeneti valószínűségek, hiszen a valószínűsége „ugráló” az egyik állapotból a másikba pontosan nulla időpillanatban (a valószínűsége egy adott érték egy folytonos valószínűségi változó).
Ezért ahelyett, hogy az átmeneti valószínűségeket be véve a sűrűsége átmeneti valószínűségek:
ahol - annak a valószínűsége, hogy a rendszer pillanatnyilag abban a helyzetben, a mozgás alatt az állam.
Akár végtelenül kicsi a másodrendű a fenti képletű felírható:
Folyamatos Markov folyamat homogénnek, ha átmeneti valószínűség sűrűség nem függ az időtől (elejétől az intervallum). Egyébként a folyamatos Markov folyamatot nevezzük heterogén.
A cél a szimuláció. mint abban az esetben, szakaszos folyamatok, ez határozza meg a valószínűségeket az államok a rendszer. Ezek a valószínűségek vannak integrálva a rendszer differenciálegyenletek Kolmogorov.
Fogalmazza modellezési technika szerint a rendszer folyamatos Markov folyamatok.
- Határozzuk meg a rendszer állapotát, és a sűrűsége a átmeneti valószínűségek.
- Létrehozása és a címke az állam grafikonon.
- Olyan rendszert hozzon létre differenciálegyenletek Kolmogorov. A számú egyenlet a rendszerben az állapotok száma. Minden egyes egyenletet egy összetétele a következő.
- B bal oldalon az egyenlet van írva származékot -edik állapot valószínűségének.
- algebrai összege a tárolt termékek a jobb oldali és. A munkák száma, amíg a nyilak állapottal járó. Ha a nyíl irányított gráf ebben az állapotban, akkor a megfelelő termék pozitív, ha ki az állam - mínusz.
- Határozza meg a kezdeti feltételek és megoldani a rendszer differenciálegyenletek.
Példa 2.2. Legyen Kolmogorov differenciálegyenlet-rendszert találni a valószínűsége, hogy a rendszer állapotát, a megjelölt állam grafikon ábrán látható. 2.3.
Ábra. 2.3. Markup állami grafikon
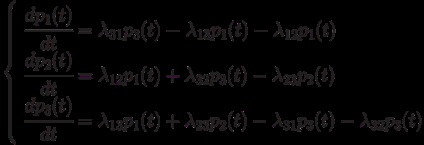
Ezért minden az első három egyenlet lehet szüntetni, mint lineárisan függ.
Hogy oldja meg a Kolmogorov egyenletek kell állítani a kezdeti feltételeket. A fenti példában 2,2, beállíthatja a kezdeti feltételek :.
Abban a vizsgálatban, összetett objektumok mindig érdekli: Lehetséges létrehozott rendszer (fix) módban? Így a rendszer működését, ha? Vannak korlátozások? Általános szabály, hogy ezek a határok érdekelt kutató.
A válasz erre a kérdésre adott Markov tétel.
Ha egyforma, különálló Markov folyamat véges vagy megszámlálható államok száma minden határértékeket és azok az értékek nem függ a kezdeti állapotban a rendszer.
Ami a folyamatos Markov folyamatok Markov-tétel a következőképpen kell értelmezni: ha a folyamat egységes és egy átmenet minden állam véges idő alatt, hogy minden más állami, valamint az államok száma megszámlálható vagy véges, akkor a határértékek léteznek, és azok az értékek nem függ a kezdeti állapot.
Például (. 2.4 ábra), A-rendszerben stacionárius rezsim, és a rendszer stacionárius üzemmódban nem: ha a rendszer olyan állapotban van, nem tudott menni bármely más állapot.
nagyobb kép
Ábra. 2.4. Példák az állam grafikonjait rendszerek különböző módok
2.3. Rendszer a születés és halál
Gyakran rendszerek különböző alkalmazások folyamatok játszódnak le, ami lehet, mint egy modell a „születés és halál”.
A grafikon Államok E folyamat ábrán látható. 2.5.
Jellemzője ennek a modellnek a jelenléte az előre és hátra kapcsolatokat valamennyi szomszédos állam mindenki számára másodlagos körülmények között; Az első és az utolsó (utolsó) összefüggő állapot csak egy „szomszéd” (a későbbi és korábbi állapotait, sorrendben).
Modell neve - „születés és halál” - együtt jár a gondolat, hogy a jobb nyíl jelzi, az átmenet az állam társított egyre több állam ( „születési”), és a nyilak balra - csökkenő számú államok ( „halál”).
Nyilvánvaló, hogy a stacionárius állapotban a folyamat létezik. Kolmogorov egyenlet nem lehet szükség, mert a szerkezet szabályos, a szükséges képleteket adjuk a hivatkozásokat, valamint az ajánlott irodalmat.
Az ábrán látható. 2.5 elnevezések képletek van formájában:
Példa 2.3. Van egy rendszer két azonos és párhuzamosan dolgozó számítógépek.
Ez szükséges, hogy meghatározzák a megbízhatóság jellemzői ennek a rendszernek.