Hozzáadása erők irányított szögben egymáshoz

A 21. § megvizsgáltuk a leírás hatása van a szervezetben két erő, ha ezek mentén hatnak ugyanazon a vonalon, megtanulták, hogy kiszámítja a kapott ilyen erők.

Gyakran azonban a testen, számos más szervek, és ezek hatása irányul különböző szögekben egymáshoz (1. és 2. ábra):

Lehetséges, hogy meghatározza egy ilyen erő, és úgy vélik, a kapott erők irányította szögben egymáshoz?

A kérdés megválaszolásához térjünk vissza a kísérletet. Két dynamometers horgok hurkokkal gyűrűt úgy, hogy ki vannak téve a gyűrű szögben egymáshoz. Ennek kompenzálására a hatásoknak a két erő teszi az ellenkező oldalon a harmadik cella és erősít a leolvasott (3. ábra):

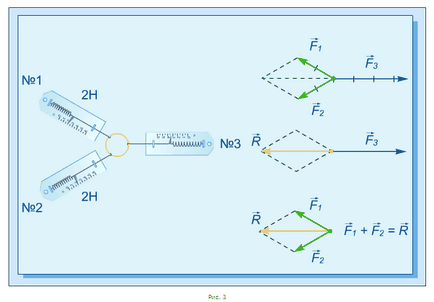
Kiderült, hogy nem olvassa a próbapadon a 3. számú, azaz a számértéke erő olyan, hogy a hossza állítható elő építve vektorok a számok az ábrán látható. Egy ilyen alak négy szög kapott transzfer vektorok párhuzamosan is, és ezért nevezik paralelogramma. Továbbá, az ilyen minta figyelhető bármilyen szögben közötti erők és bármely numerikus értékek ezen erők. A tulajdonságok ilyen négyszög paralelogramma akkor tanulni geometria órák. Egy összekötő szakasz a csúcsok átellenes sarok úgynevezett átlós a paralelogramma.

Így a számértéke erő mindig egyenlő a átló hosszát a paralelogramma által alkotott vektorok, amelyek hossza, mint tudjuk, vannak jelei dynamometers méretarányos № № 1 és 2.

Mivel erő képes kompenzálni az erő ellentétes irányú és az egyenlő erő, ez azt jelenti, hogy a termelt energia a gyűrű ugyanazt a hatást, mint a két erő, hogy egy nagysága ezen erők eredője. Így a kísérlet adja a szabályt:

A kapott a két erő irányított szögben egymáshoz, arra irányul, az átló mentén a paralelogramma épített ezek a vektorok mindkét oldalán, és numerikusan megegyezik a hossza az átló a paralelogramma.

Az eredő erő az úgynevezett erők összege.

Ez a szabály az úgynevezett szabály a paralelogramma a vektor kívül.

Ábra. A 4. ábra az építőiparban a vektor eredője az erők a különböző esetekben: amikor az erőt szögben 90 ° (ábra 4a és b.), Ezzel hegyesszöget (4. ábra, d.) És tompa (4. ábra g, azaz.) Szögben egymáshoz.

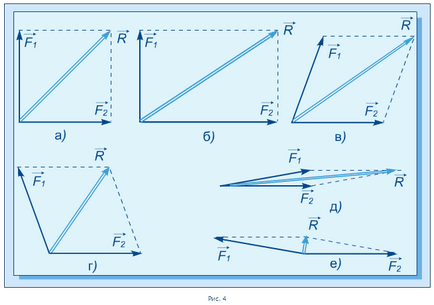
A 4d és 4e azt jelzik, hogy a paralelogramma-mozog mellett jogi erők irányított egy egyenes vonal (21. §), ha a szög vektorok között közel 0 ° (vektorok az egyik oldalra irányítja), vagy 180 ° (a vektorok irányulnak ellentétes irányban) .

A paralelogramma igaz minden vektor fizikai mennyiségek, nem csak az erő vektorok, így a matematikában is nevezik a szabály vektor összeadás. Azonban meg kell érteni a kapcsolatot vektor fizikai mennyiségek valós jelenség írnak le. Például, ha van két ható az eredeti test nyugalomban, az irányt a kapott megtalálható a paralelogramma szabály azt, ahová irányította a nettó hatása a két erő, vagyis ha mozog a test nyugalomban.

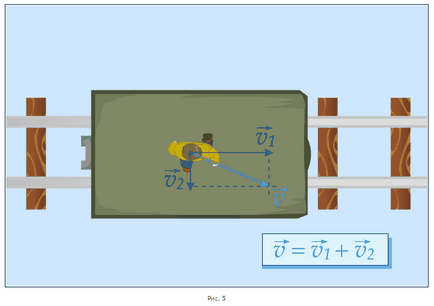
Használhatja a szabály a paralelogramma és kiegészítve a sebesség vektorok. Például, ha a vasúti peron mentén mozog a sínek a sebesség, és az ember megy a platform sebességgel, arra merőlegesen, úgy, hogy a sebesség vektorok által paralelogramma szabály, hogy lehet találni olyan vektor, hogy van, hogy megtudja, milyen irányba az érintett személy egy ilyen összetett mozgás, viszonyítva mozog a föld (ábra. 5).

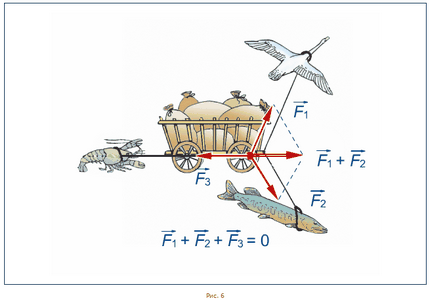
Összefoglalva, azt látjuk, hogy alkalmazásával a szabály a paralelogramma többször lehet adni, és három, és nagyobb mennyiségű erőt. Ehhez megtalálják a szabály a paralelogramma az összeget a két erő, majd a kapott vektort meghatározni a szabály a paralelogramma egy harmadik vektort. Például, ábrán. 6. azt mutatja, hogy egy hattyú vita, a rák, és a csuka nincsenek győztesek, mint a kapott, a három erő hat, a kosár, nullával egyenlő, vagy, más szóval, a keletkező erők, amelyek leírják a hatását egy Swan és csuka, egyenlő és ellentétes irányú erő-nes hatásokat.