Az egyenlet a törzs kompatibilitás
A probléma a kompozit rúd
Kanonikus egyenletek a módszer erők
Módszerek közzétételi statikus határozatlanság
Leggyakrabban a nyilvánosságra hozatal a redundancia (problémamegoldás) erőt fejt ki módszert. Ennek lényege a következő: amellett, hogy a mérleg álló független egyenletet statikailag határozatlan rendszer mentes a további kötvényeket, és a működésükkel helyébe az erők és nyomatékok erők. Az értékek az erők (nyomatékok) van kiválasztva, hogy megfeleljen a mozgás által előírt korlátozások a kapcsolat megszakadt. Itt az ismeretlen - erejét, így - „módszert erők.” Vannak más módszerek is, például a helyettesítési módszer, amelyekben az ismeretleneket nem fogadja erőt és az elmozdulást rudak.
Problémákat megoldani, a további kapcsolatok eredő állapot törzs kompatibilitás. Például, ha amellett, hogy a statikus egyenletek Sx = 0 Sy = 0, SM = 0 ADD egyenlet törzs kompatibilitás
Amikor az Erő legyen kényelmes egyenletek meghatározásához ismeretlen egyenletesen formájában úgynevezett „kanonikus” egyenletek.
Jelöljük dik kölcsönös elmozdulás rendszer a pontokat, ahol
i - az első indeks- mozgásirányban,
hogy - a második index - jelölés erő okozta elmozdulás.
Ha alkalmazzuk a szuperpozíció elve alapján, az összeget a különálló elmozdulások a fellépés az erők (beleértve reakcióelegyet elöntjük részek) nulla irányonként, például 1,2,3 tengelyek (beleértve x, y, z). Az egyenletek formája: d1 [X1, X2, ... P] = d1H1 d-1H + 2 + ... + 0 = D1R
d2 [U1, U2, ... P] + = d2U1 d2U2 + ... + D2R = 0
d3 [Z1, Z2 ... P] = d3Z1 + d1Z2 + ... + d3R = 0,
Ha X, Y, Z nem ismertek, P - adott erők.
Ha tudja, hogy bizonyos erők, a szám egyenletek csökken.
A matematikai egyenletek oldatot Dik értelemben aránya, definíció szerint az elmozdulás irányába az erő Kj 1
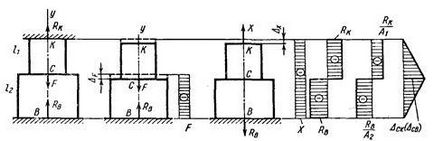
Találunk a feszültséget a rúd rögzített két részből áll. A helyszínen a COP rúd merevsége a területen E1 A1 NE - merevséget E2 A2. A statikus része a problémának azt látjuk, Sx º 0
Sy = Rk + RB - .. F = 0, azaz, feladat egyszer meghatározatlan.
Tekintsük a geometriai része a problémának. Felszabadítva a főtealátámasztó, így lehetőséget, hogy deformálja a rudat.
Munkapontja K összenyomásával a rész BC összeget DF. Reakció tartalék Rk (ismeretlen X) .Sterzhen visszatér eredeti helyzetébe a nyújtás részek nap és a SC halmozódó értéke Dx. eltávolítása D F .Ezután kompatibilitási egyenlet deformációk DF + dx = 0.
Az érték a törzs Hooke-törvény
Egyenletek megoldására a statika, megkapjuk értékek
A kapott válaszok, ebből következik, hogy a merevebb szerkezet a feltételezett nagy terhelések. Ez a tulajdonság a statikailag határozatlan rendszerek.