programozás alapjai
5.3. rekurzív módszerek
A lényeg a rekurzív módszerek - csökkentése a probléma maga. Azt már tudjuk, hogy mint a Pascal és C lehetőség van egy rekurzív függvények definiálása és eljárásokat. Ez a funkció olyan módon, hogy a program végrehajtását a rekurzív algoritmusok. Azonban, hogy a rekurzív módon oldja meg a problémát (rekurzív) gyakran nagyon nehéz.
Vegyünk egy klasszikus probléma az irodalomból ismert „című Tower of Hanoi” (ábra. 50).
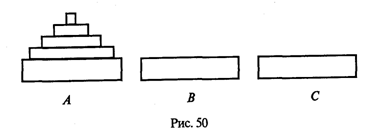
Helyben (nevezzük A) egy piramis alkotja lemezek csökkenő méretű az alaptól a felső.
Ez a piramis ugyanúgy szeretné mozgatni a helyszínen B. Az alábbi korlátozások figyelembe kell venni munkák megvalósításában:
• Egyszerre csak mozog egy lemezre, kivenni a piramis csúcsára;
• tegye a lemezt lehet akár csak a bázis terület vagy egy nagyobb lemezen;
• mint egy kiegészítő pad lehet használni S.
A név „Tower of Hanoi” származik egy legenda, mely szerint az ősi időkben, a szerzetesek a templomban jött Hanoi mozgatni ezeket a szabályokat a torony, amely a 64 lemezek. A befejezése munkájuk véget ér. A szerzetesek mindig dolgoznak, és reméljük lesz sokáig dolgozni!
Ez könnyű megoldani ezt a problémát két meghajtó. Jelző hajtás, például helyszíni B-be, mint A → B, írja az algoritmus ebben az esetben
A → C; A → B; C → B.
Csak 3 lépés! Három hosszú hajtások algoritmus:
A → B; A → C; B → C; A → B; C → A; C → B; A → B.
Ebben az esetben azt szükséges 7 mozog.
Számítsuk ki a menetek száma (N) is lehet az alábbi rekurziós képlet k lemezek:
N (1) = 1; N (k) = 2n (k - 1) + 1.
Például az N (10) = 1023, N (20) = 104857. De hány mozgások annyit kell tennie, Hanoi szerzetesek:
Próbálja olvasni ezt a számot.
Most komponálja a program, amely a gép működését algoritmus kiszámítja Monks, és megjeleníti azt bármely n értéke (a lemezek számával). Hagyja, hogy a helyszíni Egy n lemezek. Az algoritmus a probléma megoldása a következő:
1. Ha n = 0, akkor nem csinál semmit.
2. Ha n> 0, akkor mozgassa a n - 1 lemez C-tól B;
mozog a lemez A-tól B (A → B)
Mozgás n - 1 autóútra C B A.
A 2. lépésben a sorozat lesz három állapota (ábra. 51).
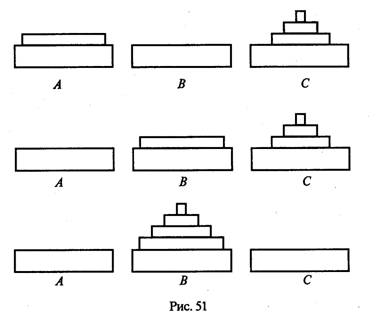
Leírás az algoritmus nyilvánvalóan rekurzív