Mi határozza meg a gép nulla, végtelen gép és a gép epszilon

Trust végzett számítás a számítógépen, árnyéka nélkül annak megértését, hogy ez a számítás elvégzése - az egyik legrosszabb dolog, ami lehetővé teszi egy mérnök munkája. Sajnos még gyakori a „szakértők”, amely nem téveszti össze nem nulla kapott eredményt megszorozzuk nulla, vagy pedig nulla, ahol a nulla elméletileg nem kellene.

Ezért ismételjük ezt a cikket néhány közhelyeknek a képviselet a valós számok a számítógép és a működési szabályairól velük.

Az IBM-kompatibilis számítógép valós számok használatával a bináris rendszer, és elfogadott egy formája ábrázolása lebegőpontos típusú x = m * 2 o. ahol mantissza m = ± (g1 * 2 -1 + G2 * 2 -2 +. + GT * 2 -t). g1. GT - bináris számjegy, sőt, g1 = 1. és p egész nevezzük bináris sorrendben. A számjegyek száma t. számára fenntartott a felvétel a mantissza nevezzük bit mantissza. A tartomány a számábrázolás számítógépes szót hossza legfeljebb véges érték a mantissza és a szám p.

Minden képviselteti magát a számítógép valós számok x kielégítik az alábbi egyenlőtlenségeket 0

Minden szám modulo -Larger X∞. Nem lehet képviselő a számítógéphez, és látta, ahogy a gép a végtelenbe. Minden szám abszolút értéke kisebb X0. A számítógép nem különbözik nullától, és látta, ahogy a gép nulla. A gép epszilon εM úgynevezett relatív pontosság a számítógép, hogy van, a határ a relatív hiba ábrázolása a valós számokat. Meg lehet mutatni, hogy εM ≈ 2 -t. Legyen x * = m * 2 o. Ezután a határ abszolút hiba ábrázolása ez a szám egyenlő a S (x *) ≈ 2 -terc-1 * 2 o. Mivel 1 / 2≤m<1. то величина относительной погрешности представления оценивается как δ(x * ) ≈ δ(x * ) / |x * | ≈ (2 -t-1 *2 p ) / (m*2 p ) = 2 -t-1 / m ≤ 2 -t-1 / 2 -1 = 2 -t.

Machinery epszilon által meghatározott bit mantissza és kerekítési módszer végre egy bizonyos számítógépen.

Az általunk használt módszerek meghatározására közelítő értékeit az ismeretlen változók:

beállítva X∞ = 2 n. ahol n - az első természetes szám, ahol túlcsordulás jelentkezett;
hagyja X0 = 2 -m. ahol m - az első természetes szám. ahol -m 2 egybeesik nulla;
tegye εM = 2 -k. ahol k - a legnagyobb természetes szám, amelynek összege a számított értéke 1 + 2 -k még mindig nagyobb, mint 1. Tény, εM a határ az a relatív hiba ábrázolása száma x * ≈ 1.

Kérdezi inkább a megfelelő környezetben (csomag), és válassza ki a beállításokat, itt egy példa az én MathCAD 15:

gép nulla, végtelen gép és a gép epszilon a MathCAD 15

És végül egy pár szabványos emlékeztető: K valódi értékek általánosan alkalmazható művelet == ( „összehasonlítás”) miatt pontatlan ábrázolása ezeket az értékeket a számítógép memóriájában. Ezért, az igazi változó arányát alkotnak == b általában helyébe FAB (a-b) ≤eps. ahol FAB () - funkciója valós szám számítási modult és EPS - kis értékű, meghatározza megengedett hiba. Hibahatáron vihetők be a számítás, mint a standard kerek kerekítési módszer, például a számítás a bal termék a számok MathCAD nem karcolja, és a jog - igen:

Mi határozza meg a gép nulla, végtelen gép és a gép epszilon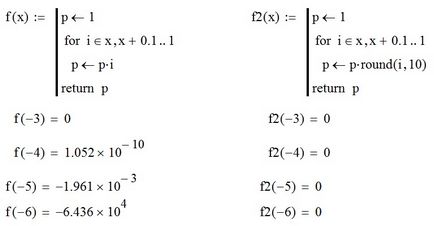

könyvelési hibák forduló során módszer (Mathcad)

Kapcsolódó cikkek

előző ◈ a következő