Symmetry pont körül, a fő portál tanul
Szimmetria a lényeg
Legyen G - fixpont és X - véletlenszerű pont a síkban (lásd ábra 187.). Mi elhalasztja a meghosszabbítása a szegmens OX az O pont szegmens OX”, egyenlő OX.
Point X 'nevezzük szimmetrikus pont X viszonyítva, hogy a pont A. A pont szimmetrikus O pont az nagyon pont O. Nyilvánvaló, hogy egy pont szimmetrikus arra a pontra X', egy pont X.
Konverzió számadatok ábrán F F „ahol minden egyes pont X válik egy pont X”, amely szimmetrikus egy adott pont O nevezik szimmetria transzformáció tekintetében a pont O. Ebben az esetben, F és F „a szám azt mondják, hogy szimmetrikus az O pont (ábra. 188).
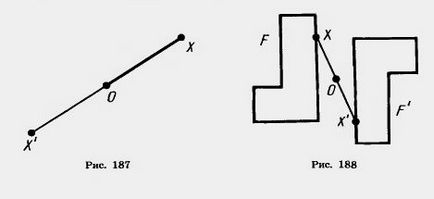
Ha a szimmetria transzformáció tekintetében az O pont kialakul F egy, ez nazyvaetsyatsentralno szimmetrikus. és a G pont a központja a szimmetria.
Például, egy paralelogramma központosán szimmetrikus alakja. A közepe szimmetria metszéspontja az átlók (ábra. 189).
Tétel 9.2. Átalakulási pontja szimmetria a mozgás.
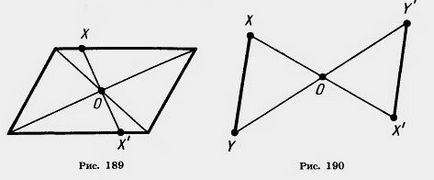
Bizonyítás. Legyen X és Y - két tetszőleges pont az ábra F (190 ábra.). Conversion szimmetria pont körüli O továbbítja azokat a pontokat X „és Y
Tekintsük háromszögek XOY és X'OY”. Ezek háromszög egyenlő az egyenlőség elve alapján az első háromszög. Ezek bezárt szöge kb mind függőleges, mind OX = OX „OY = OY” definíció szerint szimmetria pont körül O. A egyenlőséget a háromszögek kell a fegyverek egyenlősége: XY = X'Y”. Ez azt jelenti, hogy a szimmetria O pont mozgását. Ez azt bizonyítja, a tétel.
A. V. Pogorelov, geometria évfolyamon 7-11 tankönyv oktatási intézmények