Pont és intervallum előrejelzések a pár regressziós modell

Az egyik probléma az ökonometriai modellezés megjósolni a viselkedését a vizsgált jelenség vagy folyamat a jövőben. A legtöbb esetben ez a probléma is megoldható alapján regressziós modellek, amelyek felhasználhatók megjósolni a viselkedését a tényleges változó attól függően, hogy a viselkedését tényező változó.

Nézzük az előrejelzési folyamat a lineáris regressziós modell gőzfürdőt.

Pontozás peremennoyu pont becslés alapján a lineáris regressziós modell pár egy adott tényező értéke változó Xm hajtjuk a következő képlet:

Point predikciós hatékony változó ym megbízhatósági szint γ, vagy (1-a) esik az intervallum becslés, meghatározása a következő:

T - T-kritérium Student, amely attól függően van meghatározva előre meghatározott szignifikancia szinten, és a szám a szabadsági fokok (n-2) egy lineáris regressziós modellt gőzt;

ω (m) - predikciós hiba értéke az M pont.

A lineáris regressziós modell gőz predikciós hiba értéke határozza meg a képlet:

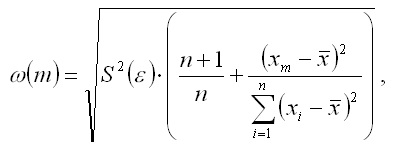
ahol S2 (ε) - torzítatlan becslése a variancia a véletlen hiba a lineáris regressziós modell pár.

Tekintsük a meghatározásának folyamata a predikciós hiba értéke β (m).

Tegyük fel, hogy az alapján a minta adatot épített lineáris regressziós modell gőzfürdő típusok:

X faktor változó a modellben bemutatott egy középre formában.

A probléma abban áll, kiszámításakor hatékony előrejelzése y adott tényező értéke változó Xm, t. E.

Az elvárás hatékony y változó m kiszámítása a képlet:

Diszperziós hatékony y változó m kiszámítása a képlet:

ahol a D (β0) - diszperziós paraméter becslés β0 lineáris regressziós modell gőzt, amelynek kiszámítása a következő képlettel:

Következésképpen, a lényeg becslés az előrejelzés változó tényleges pontnál m van egy normális eloszlású elvárás

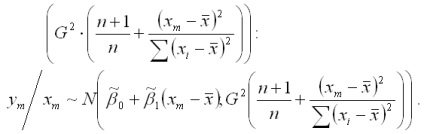
Ha az effektív változót diszperziót képlet az M pont a helyén a diszperzió G2 helyettesítheti azt szelektíven értékelési S2, akkor megkapjuk a megbízhatósági intervallum a hatékony előrejelzése y adott tényező értéke változó Xm:

ahol a mintát becsült számát variancia S2 egy lineáris regressziós modellt gőzt képlettel számítottuk ki:

Ebben az esetben az előrejelzés intervallum lehet alakítani:

QED.