Mátrix esetén - studopediya
Ha azt mondjuk, hogy a széle g és az egyes csúcsok u és y incidens g. Ez csak a költségek, ha g összeköti u és y. Miután tisztázta ezt, nézzük ezt a módszert. Az előfordulási mátrix alapján egy hasonló, de nem azonos elven, hogy a szomszédsági mátrix. Így, ha az utóbbi a mérete n × n. ahol n - a csúcsok száma, az előfordulási mátrix - n × m. itt N - a csúcsok száma, m - az élek számát. Tehát most, hogy az értéket a cella, akkor nem társítani a tetején a tetején, és a tetején a borda.
Mindegyik mátrix esetén egy irányítatlan gráf a cella van beállítva, hogy 0 vagy 1, és abban az esetben egy irányított gráf. készült 1, 0 vagy -1. Ugyanez, de strukturált:
1. irányítatlan gráf:
· 1 - a felső széle az esemény;
· 0 - vertex nem esetet a szélét.
2. irányított gráf:
· 1 - csúcsban incidens a szélére, és ez a kezdet;
· 0 - vertex nem esemény, hogy a szélén;
· -1 - vertex incidens szélén, és annak vége.
Mi konstrukció első előfordulási mátrix egy irányítatlan gráf (ábra. 3.10), majd a digráf (ábra. 3.11). Bordák jelöli a betűk A-E, a felső - számok. Minden szélei a gráf nem orientált, azonban előfordulási mátrix töltött pozitív értékek.
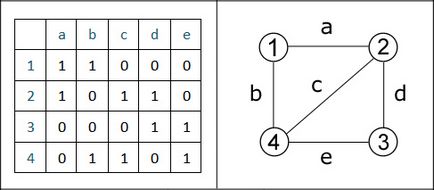
3.10 ábra - irányítatlan gráf és annak előfordulási mátrix
A digráf mátrix egy kicsit más formában. Az egyes cellái készült három érték egyikét. Felhívjuk figyelmét, hogy a nullák a két mátrix elfoglalja az ugyanabban a helyzetben, mivel mindkét esetben a gráf struktúra egyedül. Azonban, néhány pozitív egységek visszatettük a negatív, például, egy irányítatlan gráf cella (1, b) tartalmaz, 1 és -1 a digráf. A tény az, hogy az első esetben borda b irányul, és a második - irányban, és a tetején a bejárat ez a csúcs a „1”.
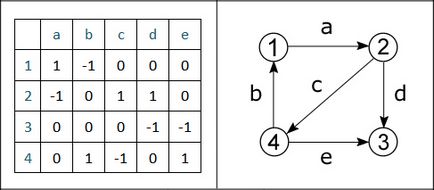
3.11 ábra - irányított gráf és annak előfordulási mátrix
Minden oszlop felel minden egyik szélét, így a grafikon leírtuk a mátrix esetén, mindig a következő jellemző: az egyes oszlopok a előfordulási mátrix két egység, 1 vagy -1, ha orientált szélén, a többi része - nullák .