Mátrix algebra - mátrixot
Mátrix algebra - mátrixot
mátrixot
Mátrixot, széles körben használják a különböző matematikai problémákat. Például, ezek alapján a jól ismert a Gauss (ismeretlen eliminációs módszerrel) megoldani egy lineáris egyenletrendszer [1].
Elemi átalakítások közé tartoznak:
1) a két permutációs sorok (oszlopok);
2) megsokszorozódása elemek az összes sort (oszlopok) mátrix számos nem egyenlő nullával;
3) Az elegyhez két sor (oszlopok) a mátrix szorozva azonos számú nullától eltérő.
Két mátrix nevezzük egyenértékű. ha egyikük lehet beszerezni a másik után véges számú elemi transzformációk. Az általános esetben nem egyenlő azzal egyenértékű mátrix, de azonos értékű.
Számítási meghatározói keresztül elemi transzformációk
Elemi átalakítások könnyen kiszámítható a meghatározója a mátrix. Például kell számítani a meghatározója a mátrix:

ahol ≠ 0.
Aztán lehet, hogy egy szorzó.

Most, kivonva az elemei j - edik stolbtsasootvetstvuyuschie elemei az első oszlop szorozva, megkapjuk a determináns:
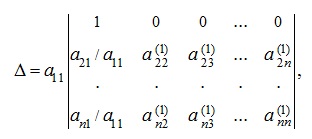
amely egyenlő: ahol
Ezután ismételje meg a lépéseket, és ha minden elemét, majd végül megszerezni:
Ha bármilyen köztes meghatározó kiderül, hogy a bal felső cella. meg kell átrendezni sorok vagy oszlopok VTAK az új bal felső tag nem nulla. Ha Δ ≠ 0, akkor az mindig el kell végezni. Meg kell jegyezni, hogy a meghatározó a jel változik attól függően, melyik elem a fő (azaz amikor a mátrix átalakul úgy, hogy). Ezután a jel a megfelelő determináns.
Példa Példa. Elemi mátrix transzformációk vezet
háromszög alakú.
. R e w n e első megszorozzuk az első sorban 4 és a második (-1), és adjunk hozzá az első sor a második:
Most szorozzuk az első sor 6, és a harmadik a (-1), és adjunk hozzá az első sor a harmadik:
Végül a második sorban szorozza 2 és a harmadik (-9), és adjunk hozzá egy második sort a harmadik:
Az eredmény egy felső háromszög mátrix