Mátrix algebra - az inverz mátrix
Mátrix algebra - inverz mátrix
Inverz mátrix egy mátrix, amely, ha megszorozzuk, mind jobb és bal oldalán ez a mátrix ad az identitás mátrix.
Jelöljük a fordított mátrix Egy, hogy a mátrix révén, majd a definíció szerint kapjuk
ahol E - az identitás mátrix.
A négyzetes mátrix nevezzük nonsingular (nem degenerált), ha determinánsa nem nulla. Egyébként ez az úgynevezett speciális (degenerált) vagy egyéni.
A következő tétel érvényes: minden nem-szinguláris mátrix inverz mátrixot.
A művelet a megállapítás a fordított mátrix nevezzük mátrix inverziós. Tekintsük azt az algoritmust inverzió. Legyen egy nonsingular mátrix n-edrendű:

ahol Δ = det A ≠ 0.
A kofaktor elementamatritsy n -edik érdekében Egy veszünk egy bizonyos jele determinánsa (n -1) -edik érdekében kapott törlésével az i -edik sor és j -edik oszlopa a mátrix A.

Forma az úgynevezett adjoint mátrix:

valahol megfelelő kofaktorokat elementovmatritsy A.
Megjegyezzük, hogy a kofaktorok az elemek a sorok az A mátrix vannak elrendezve a mindenkori oszlopok a mátrix. azaz, ugyanabban az időben készített egy mátrixot transzponáltat.
Elosztjuk minden eleme a mátrix a Δ - értéke a meghatározója a mátrix szerezni eredményeként a fordított mátrixba:
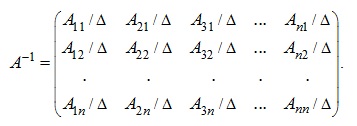
Megjegyzés néhány speciális tulajdonsága az inverz mátrix:
1) egy adott mátrix csak a fordított mátrixba;
2) ha van egy inverz mátrixot, a jobb és a bal fordított a fordított mátrix egybeesnek azt;
3) Speciális (degenerált) négyzet mátrixot nincs fordított mátrixba.
A fő tulajdonságai a fordított mátrixba:
1) a meghatározója a fordított mátrix és a determináns, az eredeti mátrix reciprokok;
2) inverz négyzetes mátrix terméke mátrixok proizvedeniyuobratnyh tényezők, hozott fordított sorrendben:
3) a transzponáltját fordított mátrix megegyezik a fordított mátrixba által transzponáltját a mátrix:
Példa Példa. Számoljuk a fordítottja:
. R e w n e meghatározója a mátrix egyenlő:
Következésképpen, az A mátrix nonsingular. Adjungált mátrix A jelentése:
Felosztása az összes elem csatlakozik a mátrix Δ = 1, megkapjuk a fordított mátrix:
Azt ellenőrzik, hogy valóban,
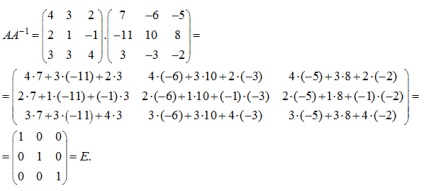
Így a fordított mátrixban találhatók egy adott mátrix