Lab № 3 mérési csúszásérték
számítás:

Kiszámítjuk a relatív hiba:
mert
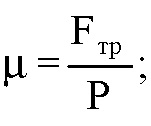
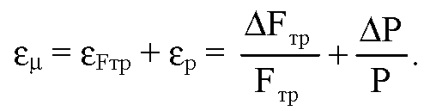
Ez azt mutatja, hogy a legnagyobb relatív hibája a kísérletben a legalacsonyabb terhelés, mivel a nevező kisebb, mint
Kiszámoljuk az abszolút hiba
mert
Ez azt mutatja, hogy a legnagyobb relatív hibája a kísérletben a legalacsonyabb terhelés, mivel kevesebb, mint a nevező.
Kiszámoljuk az abszolút hiba
eredményeként kapott kísérletek csúszó súrlódási együtthatót a következőképpen írható fel: μ = 0,35 ± 0,05.
Ha nincs megoldás erre a problémára - ne aggódj. A rendszergazdák próbálják kiegészítik a helyszínen megoldás ezekre a problémákra, és gyakorlatot, ahol szükséges, és amelyek nem szerepelnek Reshebnik és a gyűjtemények a GDZ. Próbálja újra később. Valószínűleg találja, amit keres :)
Örömmel üdvözöljük a diákok minden oktatási intézmények minden korosztály honlapunkon! Itt található Reshebnik és megoldani a problémákat ingyen, regisztráció nélkül.
davay5.com