Kihívások a bizonyítási
A trapéz KLMN szárnyon KL merőleges az alapra. A K pontot oldalán a merőleges csökkent MN KA. Az oldalon KL jelölt B pont úgy, hogy a vonalak LA és BN párhuzamosak.
a) Igazoljuk, hogy a BM és MN merőlegesek.
b) Find aránya LA: BN, ha a szög egyenlő LMN 150 ^.
a) Annak bizonyítására, merőleges egyenesek BM és az MN elegendő annak bizonyítására, hogy a BM \ párhuzamos KA, és ez történik, ha a hasonló háromszögek SBM és SKA. azaz, ha az egyenlőség \ frac = \ frac.
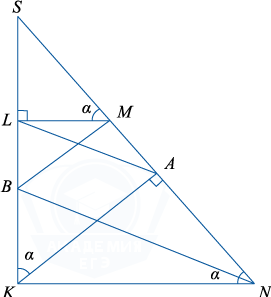
Let \ szög SKH = \ alpha. Ezután \ szög SKA = \ szög ANK = \ alpha. A párhuzamos vonalak LA és BN, ebből következik, hogy a háromszögek hasonlóak SLA és SNB, akkor az egyenlőség \ frac = \ frac.
Egy derékszögű háromszög SLM. \ Frac = \ sin \ alpha. ahol SM = \ frac.
Egy derékszögű háromszög SAK. \ Frac = \ sin \ alpha.
Egy derékszögű háromszög SKN. \ Frac = \ sin \ alpha. SK = SN \ sin \ alpha.
Megszorozzuk egyenlet \ frac = \ sin \ alpha és \ frac = \ sin \ alpha. kapjuk: \ frac = \ sin ^ 2 \ alpha. SA = SN \ sin ^ 2 \ alpha. Tekintettel arra, hogy \ frac = \ frac hoztunk \ frac = \ sin ^ 2 \ alpha. ahol SB = \ frac.
\ Frac = \ frac = \ frac. Jobb oldalán egyenlő, tehát, \ frac = \ frac, majd egyenesen LA és BN párhuzamosak, és merőlegesek a BM és MN.
b) Tekintettel a hasonlóság SML és SKN háromszögek. \ Frac = \ frac.
Amint az a). \ Frac = \ sin ^ 2 \ alpha. A hipotézis \ szög LMN = 150 ^, \ szög LMN + \ alpha = 180 ^, \ alpha = 180 ^ -150 ^ = 30 *.
\ Frac = \ sin ^ 2 \ alpha = \ sin ^ február 30 ^ = \ frac14.
Munka típusa: 16
Tárgy: Kihívások a bizonyítási
Két kört központok O_ O_ és rendre vonatkoznak külsőleg. O_K tartott érintkeznek a második kört egy pont O_ (K - Touch Point). pontjától és O_ O_L tartott érintő első kör (L - Touch Point). érintse pont K és L hazugság különböző oldalain vonal O_O_.
a) Bizonyítsuk be, hogy \ angle O_KL = \ angle O_O_L.
b) Find a sugara a kisebb kör, ha járulékosan ismeretes, hogy az a 4-szer kisebb, mint a sugara a nagyobb kört, egy négyszög O_KO_L terület 54 + 9 \ sqrt.
a) A tulajdonát érintő a kerülete O_L \ elkövető O_L és O_K \ elkövető O_K. Négyszög \ bigtriangleup O_O_K írt kör átmérője O_O_.
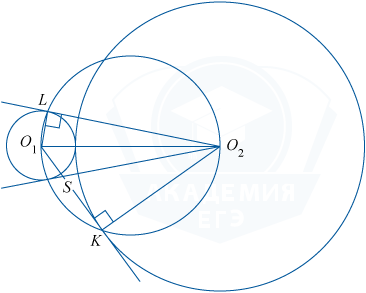
Hasonlóképpen, téglalap alakú \ bigtriangleup O_O_L írt egy kört azonos átmérőjű. Ezért, \ bigtriangleup O_O_K O_O_L és feliratos ugyanabban kör, hogy az a pont a O_, O_, K. L egy körön átmérőjű O_O_. Tehát \ angle O_O_L és \ angle O_KL - feliratos és alapul az azonos ív O_L. Ennélfogva, \ szög O_KL = \ szög O_O_L.
b) Legyen O_L - sugara kisebb kör. Jelöljük r. Következésképpen, O_K = 4r. Ezután O_O_ = r + 4r = 5R. Ennélfogva, a \ bigtriangleup O_LO_ Pitagoraszi O_L = \ sqrt = 2 \ sqrtr. Feladó \ bigtriangleup O_KO_ Pythagorean O_K = \ sqrt = 3r.
A feltétel az következik, hogy S_KO_L> = 54 + 9 \ sqrt. Ezután (6+ \ sqrt) r ^ 2 = 54 + 9 \ sqrt, (6+ \ sqrt) r ^ 2 = 9 (6+ \ sqrt), R = 3.
Munka típusa: 16
Tárgy: Kihívások a bizonyítási
Két tetszőleges kört érintik egymást, vannak írva egy előre meghatározott szögben, a értéke \ alpha. nem haladja meg a \ pi.
a) Bizonyítsuk be, hogy az arány a sugarak különbsége modul összege sugarak e körök állandó.
b) Find a sugara a kisebb kör, amikor a szög \ alpha = \ frac és sugara a nagyobb kör 10.
a) jelöli előre meghatározott szögben keresztül ABC. sugarak a körök R_ és R_ (R_ Mivel a központok a körök egyforma távolságban van a oldalán a szög, fekszenek a szögfelező B. Draw központja a körön O_T és O_E a érintési pontján az oldalsó AB.
Ezután O_T O_E és merőleges AB.
A központ a kisebb kör O_ kihagyja merőleges O_K O_E sugara nagyobb kerületű. Kapunk egy téglalap O_TEK. Ezután EK = TO_ = R_. Következésképpen, O_K = O_E-KE = R_-R_.
Mivel O_K \ párhuzamos AB-vel. hogy \ szög ABO _ = \ angle KO_O_. Megjegyezzük továbbá, hogy O_O_ = R_ + R_.
Ebből következik, hogy \ frac-r _> + r _> = \ Frack> O _> = \ sin \ szög KO_O_ = \ sin \ szög ABO_.
De \ szög ABO _ = \ frac, ahol \ alpha - előre meghatározott szögben, így \ frac-r _> + r _> = \ sin \ frac.
b) Behelyettesítve a megadott értékek \ alfa és R_ általános képletben fentiekben kapott, kapjuk:
Munka típusa: 16
Tárgy: Kihívások a bizonyítási
A bázis CD trapéz ABCD merőleges a BC oldalt. Keresztül a pont, A és D volt egy kör, amely érinti a BC egyenest a ponton M.
a) Bizonyítsuk hasonlóság \ bigtriangleup ABF és a \ bigtriangleup FBK, feltéve, hogy az F - átkelőhely a vonalak BC és az AD. és BK - magassága \ bigtriangleup ABF.
b) Feltéve, CD = 4 cm, és AB = 5 cm, kiszámítja a távolságot az M pont az AD vonal.
Az általánosság elvesztése nélkül, mondhatjuk az egyik lehetséges konfigurációk:
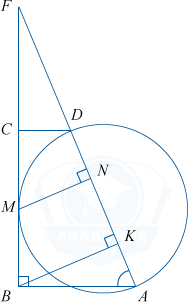
a) Magasság \ bigtriangleup ABF \: BK \ elkövető AF \ Rightarrow \ bigtriangleup ABF és \ bigtriangleup FBK - téglalap alakú, ezek hasonlóak (egy általános F szög).
b) Rajzold MN \ elkövető AD. Ezután MN - távolság az M pont, hogy a vonal AD.
\ Bigtriangleup ABF, \ bigtriangleup MNF, \ bigtriangleup CDF - téglalap alakú, a hegyesszög F - általában, így ezek hasonlóak.
\ Bigtriangleup MNF \ sim \ bigtriangleup ABF \ Rightarrow \ frac = \ frac, MN = \ frac.
\ Bigtriangleup MNF \ sim \ bigtriangleup DCF \ Rightarrow \ frac = \ frac, MN = \ frac.
A tétel a metsző és érintő, van:
FM ^ = AF \ cdot FD. Ezután MN ^ = AB \ cdot CD = 20.