E (szám)
[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, ...]
(Ez a folyamatos tekercs nem periodikus. Felvett lineáris jelöléssel)
Az első 1000 tizedesjegy e [1]

A terület a diagram alatt y = 1 / x intervallumban 1 ≤ x ≤ e értéke 1
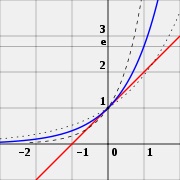
e - egy szám a. oly módon, hogy az érték a származék (a meredeksége tangens vonal) az exponenciális függvény f (x) = a x (kék) azon a ponton, x = 0 értéke 1 (piros vonal). Összehasonlításként bemutatjuk a funkció 2 x (pontozott vonal), és 4 x (szaggatott vonal); a lejtőn a érintője amely eltér 1
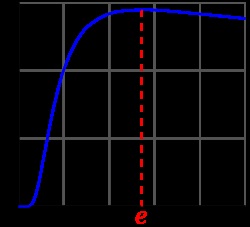
funkció maximális születik.
Mivel a függvény integrálja kitevő és megkülönbözteti „önmagában”, logaritmus, hogy az alap e venni, mint a természetes.
Meghatározására szolgáló módszereket [idézet]
A számos e lehet meghatározni többféleképpen.
- Miután a határérték (a második méltó határérték). (Stirling-formula).
- Mivel az összeg a sorozat. vagy.
- Mivel egyes szám a. amelyekre a
- Mivel csak a pozitív szám a. akinek jogát
Tulajdonságok [szerkesztés]
Ez a tulajdonság fontos szerepet játszik a megoldás, differenciálegyenletek. Például, az egyetlen megoldás, hogy a differenciálegyenlet a függvény, ahol a c - tetszőleges konstans.- Az e szám irracionális, sőt transzcendens. Ő transzcendencia bebizonyosodott csak 1873-ban Charles Hermite. Feltételezzük, hogy e - normális számot. azaz a valószínűsége különböző számot a jegyzeteit ugyanaz.
Tegyük fel, hogy a racionális. Akkor hol - egész, és - természetes.
Megszorozzuk mindkét oldalán az egyenlet így
Átviszi a bal oldalon:
Minden szempontból jobb része az egész, tehát az összeg a bal oldalon - az egész. De ez az összeg pozitív, az azt jelenti, hogy nem kevesebb, mint 1.
Másrészt,
Összefoglalva a mértani a jobb oldali, megkapjuk:
- Az e szám kiszámítható (és ennélfogva számtani) számát.
- , cm. Euler-képlet. különösen
- További képletek kapcsolatos e szám és π:
- t. n. „Poisson beépített” vagy „szerves Gauss”
- határ
- Minden komplex szám z következő egyenlőségek igaz:
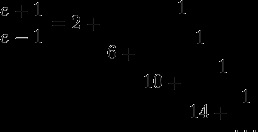
- Az e szám bontjuk végtelen lánctört a következő: azaz,

- Vagy azzal egyenértékű:

- Egy gyors számítás nagy karakterek száma sokkal kényelmesebb használni más bomlástermékek:
- Előadás a katalán.
- Előadása a terméket.
- Miután több Bell
- Mérték az irracionalitás e = 2 (ami a lehető legkisebb érték az irracionális számok). [2]
History [szerkesztés]
Az ugyanazon állandó először kiszámoltuk a svájci matematikus Bernoulli során a probléma megoldásának a mennyiségét korlátozzák kamatbevétel. Azt találták, hogy ha a kezdeti összeg $ 1 árának 100% -át évente egyszer, a az év vége, a teljes összeg lesz $ 2. De ha ugyanazt a kamatteher évente kétszer, 1 $, szorozva 1,5 kétszer, így $ 1.00 × 1.5² = $ 2.25. Érdeklődjön negyedéves vezet $ 1.00 × 1.25 = $ 2,44140625 4, és így tovább. Bernoulli megmutatta, hogy ha Kamatláb végtelenségig növelni, a kamatjövedelem esetében a kamatos kamat van egy határ. és ez a határérték egyenlő 2,71828 ...
$ 1.00 × (1 + 1/12) = 12 ... $ 2,613035
$ 1.00 × (1 + 1/365) 365 = $ 2,714568 ...
Így e egy állandó maximális lehetséges nettó jövedelem 100%, és a maximális frekvenciája kamattőkésítési [3].
Az első ismert használata a konstans, ahol betű jelöli b. talált írásaiban Huygens Leibniz. 1690 -1691 év.
Miért a levél e már kiválasztották. ismeretlen. Talán ez annak a ténynek köszönhető, hogy a szóval kezdődik exponenciális ( „demonstrációs”, „exponenciális”). Másik feltételezés az, hogy a levél a. b. c és d már meglehetősen széles körben használható más célra, és e volt az első „szabad” betűt. Azt is érdemes megjegyezni, hogy a levél e az első nevet a Euler (Euler).
Közelítése [idézet]
Nyitott problémák [szerkesztés]
- Nem ismert, hogy az időszakok száma a gyűrű.
- Nem ismert, hogy a szám az algebrai független.
- Ismeretlen intézkedés irracionalitás bármely az alábbi számok: Az egyikük sem tudja, hogy ez egy racionális szám, irracionális algebrai és transzcendens szám. [6] [7] [8] [9] [10] [11] [12]
- Nem ismert, hogy az első szám Schiusa egész.