Csebisev polinomok

Home | Rólunk | visszacsatolás
Először is, a Csebisev polinomok ilyen fontos tulajdonság, hogy ha a nemlineáris elem statikus tulajdonsággal rendelkeznek, amely a Csebisev polinom fokú N, alkalmazni a jel harmonikus, például koszinusz (sine) egység amplitúdójú, a kimenet a nemlineáris elem is harmonikus jele egység amplitúdójú, de egy N-szeres frekvenciájú.
Másodszor, a Csebisev polinomok nőnek intervallumon kívül [-1, 1] leggyorsabb az összes polinomok azonos mértékben. Ezeket használják a szintézis lineáris szűrők [2]. És ilyen szűrő egy előre meghatározott frekvenciasávot hullámosság rendelkeznek a legtöbb meredek frekvencia jelleggörbe egy csík zár képest más szűrőkkel az ugyanabban a sorrendben.
Harmadszor, a Csebisev polinomok vannak beállítva merőlegesen súlyfüggvények [1], amely lehetővé teszi, hogy például képzelni, egyedi nemlineáris statikus jellemző non-késleltetés egység formájában meglehetősen gyorsan konvergáló sorozat.
Csebisev polinomok a forma [1, 2]:
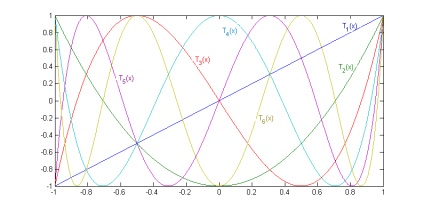
A grafikonok első öt Csebisev polinomok az alábbiak:
Ábra. 1.1. Csebisev polinomok. Csebisev polinom időintervallumra (-1, 1) értékekre korlátozott (-1, 1), és a külső és ezen intervallum növekszik nagyságrenddel gyorsabb, mint bármely más polinom azonos mértékben, korlátozza ugyanolyan állapotban
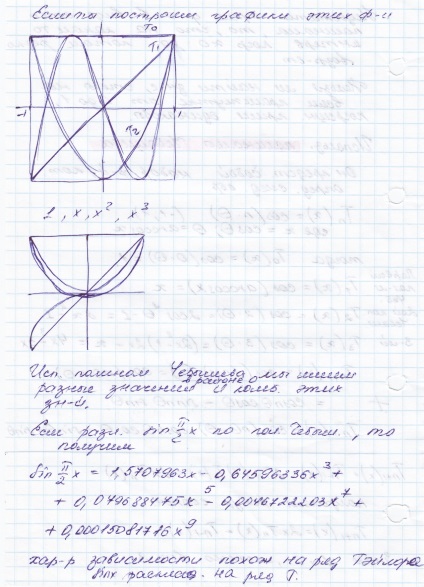
Amikor először láttam a Csebisev polinomok, majd figyelni, hogy az előadás:
hogy első pillantásra érthetetlen módon, de nagyon szép kapcsolatokat trigonometriát és algebra.
Csebisev polinomok az első fajta ortogonális függvények a rendszer és meghatározása a következő:
A reláció trigonomitricheskie koszinusz összegek és különbségek is megjelennek találni kiújulás Chebyshev polinomok:
A polinom Tn (x) intervallumban [-1,1] pontosan n gyökerek pontokban helyezkednek el,
Bármely f (x), meghatározott intervallumon [-1,1] lehet közelíteni a következő képlet szerint:






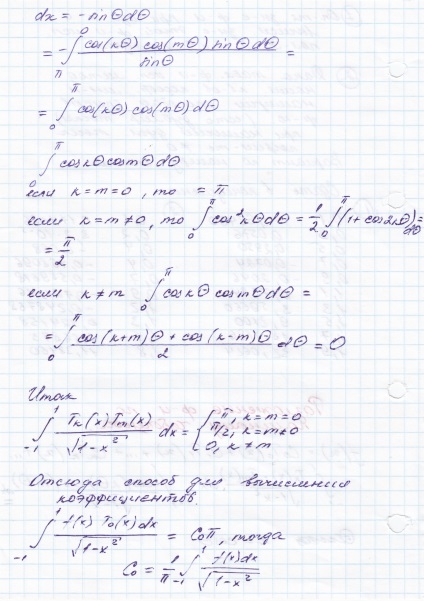

Bevezetés és racionális függvények folyamatos frakció










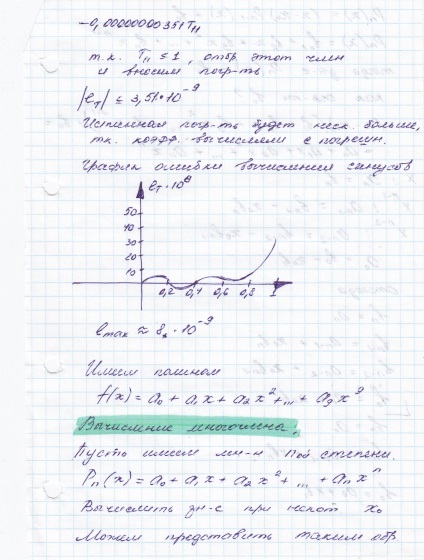
Reakcióvázlat polinom kiszámítása Horner
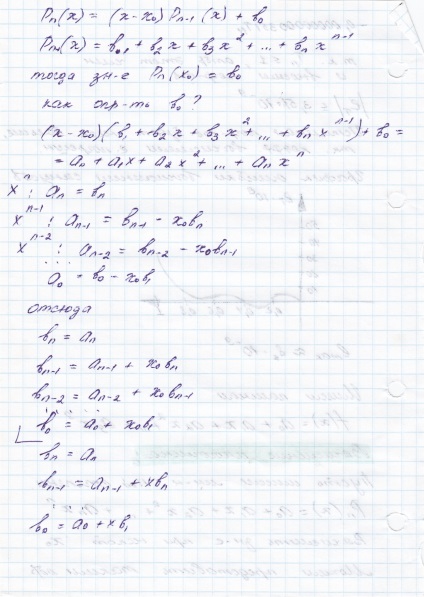
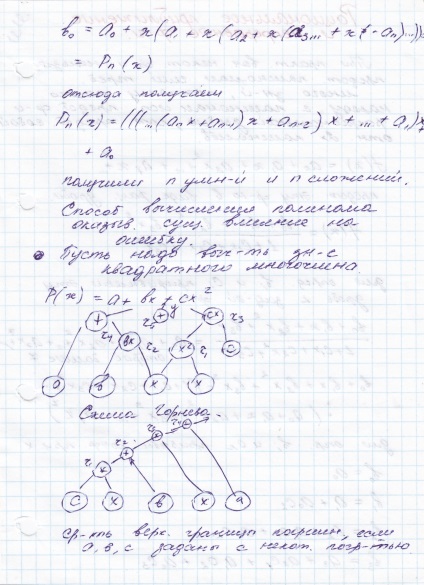




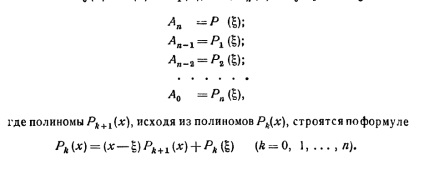


A határokat minden gyökerei a polinom
A határokat az igazi gyökere a polinom







Módszerei tisztázása valós gyökereit nemlineáris egyenletek (fele és arányos Division, Newton, egyesítjük, iteratív, usov.iteteratsii). feltétele a konvergencia a iteratív módszerek.



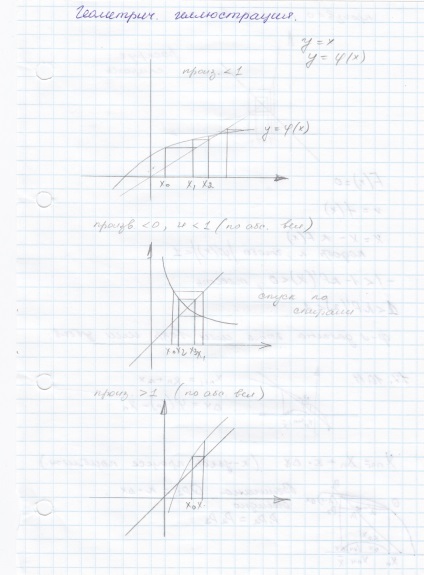



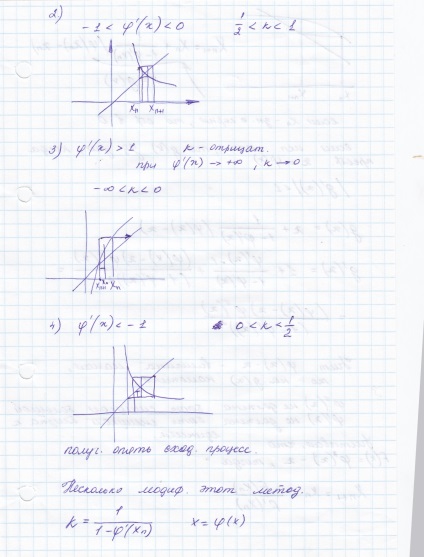




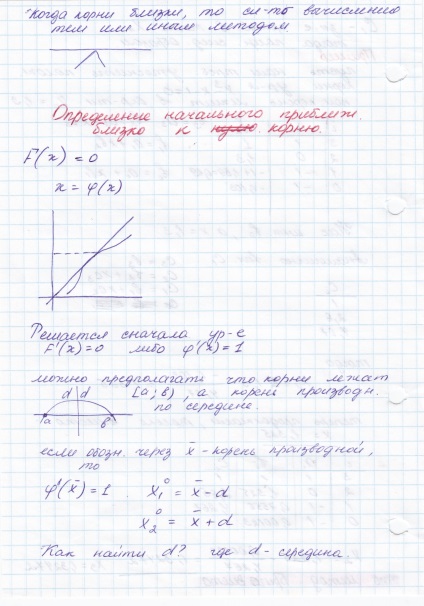
Megtaláljuk a kezdeti érték közel nulla polinom


15. Eljárás Vietti Brig-13 =