A divergencia vektor mező 1
.
15.1.4. A divergencia vektor mező
Beépített jellemzők - áramot és egy lineáris szerves - jellemzésére vektor mező „egészét”. A mennyiségi jellemző a területen, hogy minden ponton bevezetett alábbi eltérés jellemzőit. Bemutatjuk a koncepció eltérés.
Térhatású tetszőleges M pont felülete (S) tetszőleges alakú (például gömb elegendően kis sugarú). Legyen (V) - a tárolt anyag térfogata a felületen belül (S).
Definíció. A végállás arányának az áramlási mező a felület (ek), hogy a körülzárt térfogat belül történő összehúzódása a felület az M pont és a szívási térfogatú V nullára nevezzük divergenciája a vektor mező pontban M:
Megjegyzés. Definíció (1.10) invariáns (független a koordináta-rendszer) meghatározása eltérés.
Eltérés jellemzi egységnyi térfogatáram vektor mező, „kimenő” M., azaz pont forrás teljesítmény (AT) vagy a leeresztő (at) pontban M.
Egy derékszögű koordináta-rendszert az eltérés képlettel számítottuk ki
Tulajdonságok eltérés. Let - Vector Fields - skalár függvény. majd:
Tekintettel az (1.10) átírni Gauss (1.6)
- áramlási vektor mező egy zárt felület (S) egyenlő a hármas integrál térfogat (V), belsejében vannak elhelyezve a felület a divergencia a területen.
Példa 1. Számítsuk ki.
2. példa számítani, ahol u (M) - skalárfüggvény, - egy vektor funkció.
Határozat. Képlet (1.10) találunk.
Példa A 3. példában Gauss-tétel (1,12), megtalálja az áramlási vektor területen keresztül a teljes felületen (S) a test (V):
az irányt a kifelé normális.
Határozat. Van. Ezért, =. Kiszámításához a hármas integrál folytassa a hengeres koordinátákat. felülete egyenlet formájában =.
15.1.5. Rotor (vortex) vektor mező
Tegyük fel, hogy a területen - differenciálható mezőben (azaz a nyúlvány a vektor mező a koordinátatengelyeken differenciálható függvények).
Definíció. Örvény vektor mezőben (jelöljük rothadás) egy vektor, amelynek nyúlvány egy tetszőleges vektor kerül meghatározásra, mint a határérték, a területén forgalomban való összefüggése tekintetében néhány áramkör (L), amely tartalmazza azt a pontot M. és síkban fekvő merőleges a vektor, hogy a terület a régió által határolt hogy kontúr, azzal a megkötéssel, hogy a hurok szerződött ponton M. terület és a terület (S) nullához:
A háromdimenziós térben keresztül derékszögű téglalap koordinátáit vektor a következőképpen fejezhető ki:
vagy kényelmes tárolására szimbolikus formában
Stokes-tétel. Hagyja, hogy a koordinátákat a vektor + folyamatos és folytonos származékai. Azután a keringetési a vektor mező egy zárt áramkört (L) egyenlő az áramlási területen keresztül egy tetszőleges örvény felületet (S), által kifeszített hurok:
Feltételezzük, hogy a kontúr orientáció (L) és a felület (S) megállapodtak: pozitív áram utat irányul a normális „toe-to-head”.
Rotor tulajdonságok: 1); 2).
Definíció. Lehessen beállítani vektor mező nevezik a szakterületen (V), ha.
1. példa: Find a forgórész mező mágneses mező vektort.
Reshenie.Vektor koordináta formájában:
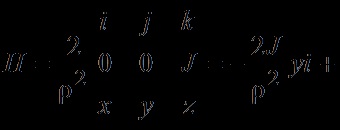
+ -
- Térerősség - lehessen beállítani a területen.
Példa 2. Számítsuk ki a vektor a keringetőkör 1) közvetlenül, 2) szerinti Stokes tétele.