02 Hogy a legnagyobb a célfüggvény
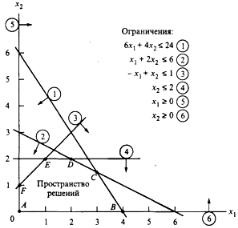
Megtalálni a maximális célfüggvény
Az általunk használt modell épül a cég Reddy Mikks, megmutatni mindkét szakaszában a grafikus megoldás az LP probléma.
1. lépés: A épület terébe megvalósítható megoldásokat.
Első sorsolás tengely jelzi a vízszintes változó értéke x 1 és
a függőleges - X 2. Ezután úgy a feltétel nem-negativitás változók: x 1, x 2, 0 és 0. Ez a két korlátok azt mutatják, hogy a tér a megvalósítható megoldásokat fog feküdni az első negyedben.
Elszámolni a még meglévő korlátozások cserélje egyenlőtlenség az egyenlőség, aminek eredményeként megkapjuk az egyenletek a sorokat, majd a gépet tart ezeket a sorokat.
Most, hogy hogyan grafikusan értelmezni egyenlőtlenség. Minden egyenlőtlenség megosztja a sík x 1 x 2 két fél, amelyeket mindkét oldalán elhelyezkedő, a vonal, amely megfelel ennek az egyenlőtlenséget. sík pont
egyik oldalán helyezkedik el az egyenes kielégítésére (fél-megengedhető), és a pontokat, hogy feküdjön a másik oldalon - nincs. „Test” pont
Ellenőrzések pont félig kielégíteni, és mi - nem,
szolgálhat az a pont (0, 0). Például, ezt a pontot kielégíti-e egy első egyenlőtlenség
X 6 x 1 április február 24 (itt 6 * 0 + 4 * 0 = 0 <24 ). Это означает, что точки полупространства,
tartalmazó kiindulási pont (0,0), kielégíti ezt az egyenlőtlenséget. Ábra. 1
megengedett félig látható nyilak.
Abban az esetben, ha a (0,0) pont nem teljesíti az egyenlőtlenséget, akkor megengedett féltér, amely nem tartalmazza a pontot. Ha a vonal áthalad ezen a ponton meg kell, mint a „teszt”, hogy bármely más kérdésben.
2. lépés: az optimális megoldás.
Pontja a tér megengedett megoldások, ábrán látható. 1, kielégíteni
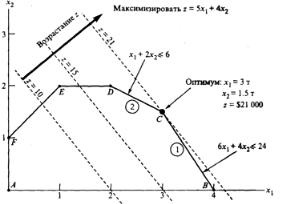
ugyanakkor az összes korlátok. Ez a tér által határolt vonalszakaszok, amelyek egymáshoz vannak rögzítve a sarokpontok A, B, C, D, E és F. Bármely pont helyezkedik el, vagy a határ a régió által határolt sokszög ABCDEF, egy lehetséges megoldás, azaz,
kielégíti az összes korlátok. Mivel a tér megvalósítható megoldásokat tartalmaz végtelen számú pontot igényel bizonyos eljárást találni az optimális megoldást.
Az optimális megoldás meghatározása szükséges a növekedés iránya a célfüggvény Z x 5 x 1 április 2-Mi lehet egyenértékű a számos z növekvő értékek, mint a 10 és 15. Ezek az értékek, a helyettesített Z helyett a kifejezésben a célfüggvény, generál az egyenletek a vonalak; A 10 és 15 értékeket az egyenlet megkapjuk a közvetlen
5 x 2 x 4 január 10. január és 4 x 5 x 2 15. ábra. 2, ezek a sorok látható szaggatott vonalak, és a
irányában növekedése a célfüggvény - a nagy nyíl. A célfüggvény növelheti mindaddig, amíg a megfelelő egyenes vonalak a növekvő fontosságát az ezt a funkciót, át a régió megvalósítható megoldásokat. A metszéspontja területének megoldásokat és a vonal megfelel annak a legnagyobb lehetséges értéke a célfüggvény,
és optimális ponton.
Ábra. A 2. ábrán látható, hogy az optimális megoldás megfelel a C pontban Ez a pont egy keresztezési pont vonalak (1) és (2), úgy, hogy a koordinátái x 1 és x 2 az oldatot egy egyenletrendszer, amelyek meghatározzák ezeket a sorokat:
A megoldás, hogy ez a rendszer x 1 = 3, és x 2 = 1,5, az értéke a célfüggvény értéke Z = 21. A kapott döntés azt jelenti, hogy a vállalat számára Reddy Mikks legjobb választás egy napi termelése 3 tonna festéket a külső, és 1,5 tonna - belső dolgozik napi jövedelme 21.000.